making a box
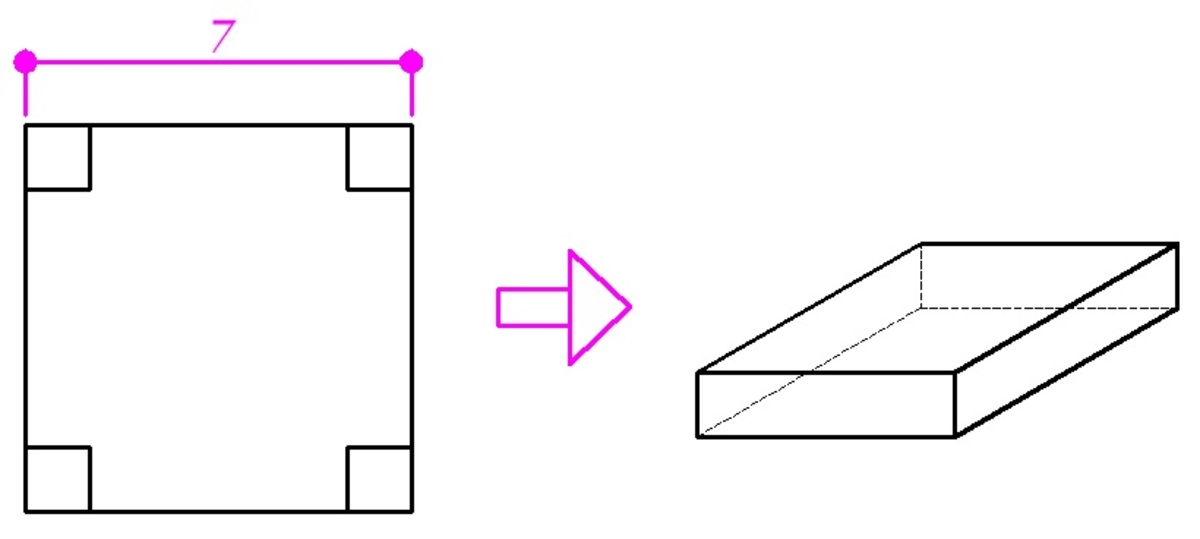A box that is open on top is to be made from a square cardboard (measuring
7
inches on each side) by cutting equal squares out of the corners and turning up the sides. Find the volume of the largest box that can be made in this way. If your answer is of the form
b
a
, where
a
and
b
are positive co-prime integers, type on the answer box the value of
a
−
b
.
The answer is 659.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
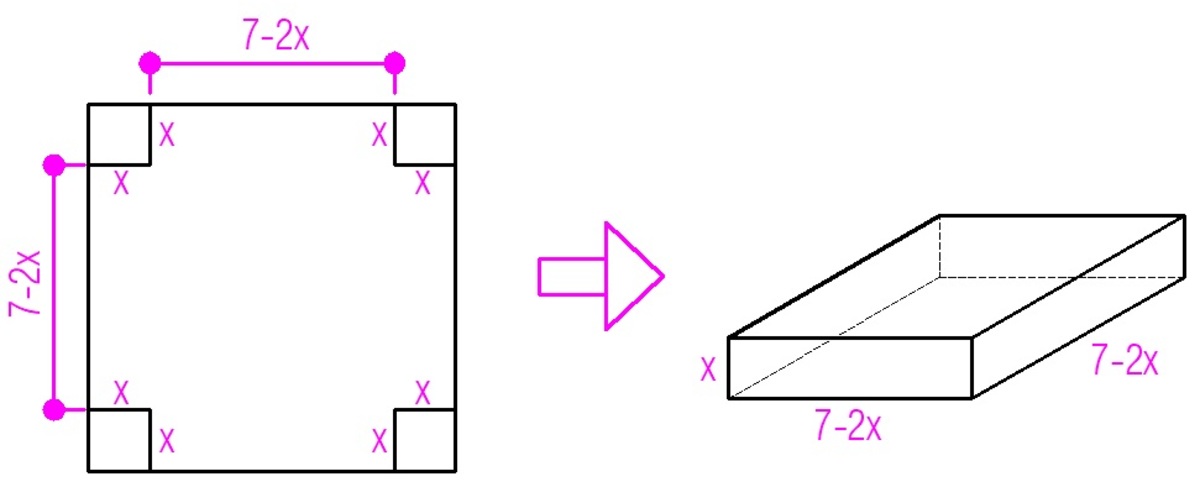Consider my diagram. The volume of the box is
v
=
x
(
7
−
2
x
)
2
=
4
9
x
−
2
8
x
2
+
4
x
3
. Differentiating both sides with respect to
x
, we get
d
x
d
v
=
4
9
−
5
6
x
+
1
2
x
2
. For
v
to be maximum,
d
x
d
v
must be equal to zero. We have,
1
2
x
2
−
5
6
x
+
4
9
=
0
. By using the quadratic formula, we get
x
=
2
7
and
x
=
6
7
. We cannot use
x
=
2
7
because the volume will be zero. So
x
=
6
7
. Thus, the desired volume is
v
=
6
7
(
7
−
2
⋅
6
7
)
2
=
2
7
6
8
6
and the desired answer is
6
8
6
−
2
7
=
6
5
9
.