Making a point
Let △ A B C be a triangle such that ∣ A B ∣ = 3 , ∣ B C ∣ = 4 and ∣ C A ∣ = 5 . Let P be any point in the triangle. If the minimum possible value of ∣ A P ∣ + ∣ B P ∣ + ∣ C P ∣ is a + b c , where a , b , c are positive integers and c is square-free, then find a + b + c .
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Such a point P is known as the first Fermat point , and is the interior point such that
∠ A P B = ∠ B P C = ∠ A P C = 1 2 0 ∘ .
Letting ∣ A P ∣ = x , ∣ B P ∣ = y and ∣ C P ∣ = z , we have by the cosine law that
9 = x 2 + y 2 + x y , 1 6 = y 2 + z 2 + y z , 2 5 = x 2 + z 2 + x z
Adding these three equations together yields that 5 0 = 2 ( x 2 + y 2 + z 2 ) + ( x y + y z + x z ) .
Now ( x + y + z ) 2 = x 2 + y 2 + z 2 + 2 ( x y + y z + x z ) , so upon substitution we have that
5 0 = 2 ( ( x + y + z ) 2 − 2 ( x y + y z + x z ) ) + ( x y + y z + x z ) ⟹
( x + y + z ) 2 = 2 5 + 2 3 ( x y + y z + x z ) .
Next, note that the area of the triangle, being right-angled, is equal to 2 1 × 3 × 4 = 6 , but that it also equals
2 1 x y sin ( 1 2 0 ∘ ) + 2 1 y z sin ( 1 2 0 ∘ ) + 2 1 x z sin ( 1 2 0 ∘ ) = 4 3 ( x y + y z + x z ) ⟹
4 3 ( x y + y z + x z ) = 6 ⟹ x y + y z + x z = 3 2 4 = 8 3 ⟹
( x + y + z ) 2 = 2 5 + 2 3 × 8 3 = 2 5 + 1 2 3 ⟹ x + y + z = 2 5 + 1 2 3 .
Thus a + b + c = 2 5 + 1 2 + 3 = 4 0 .
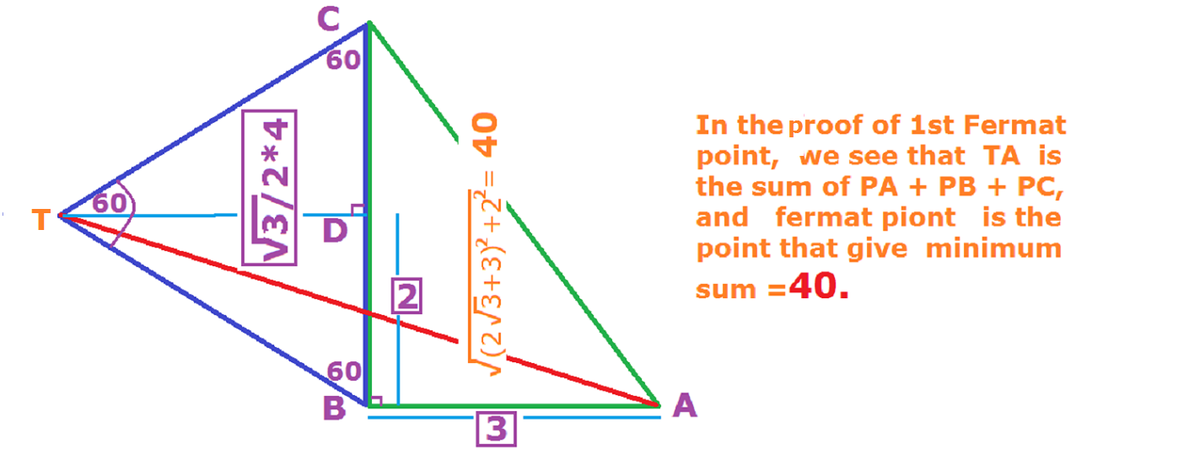
As has been shown elsewhere , the First Fermat point (or Steiner point) P can be found by constructing an equilateral triangle B C Q . Then P is the intersection of the line A Q with the circumcircle of B C Q . Moreover, A P + B P + C P = A Q .
If we set up a coordinate system with origin at B , then A has coordinates ( 0 , 3 ) , B has coordinates ( 0 , 0 ) , C has coordinates ( 4 , 0 ) , while Q has coordinates ( 2 , − 2 3 ) . Thus A Q 2 = 2 2 + ( 3 + 2 3 ) 2 = 2 5 + 1 2 3 making the answer 2 5 + 1 2 + 3 = 4 0 .