Making Molecules

Probability Level 5

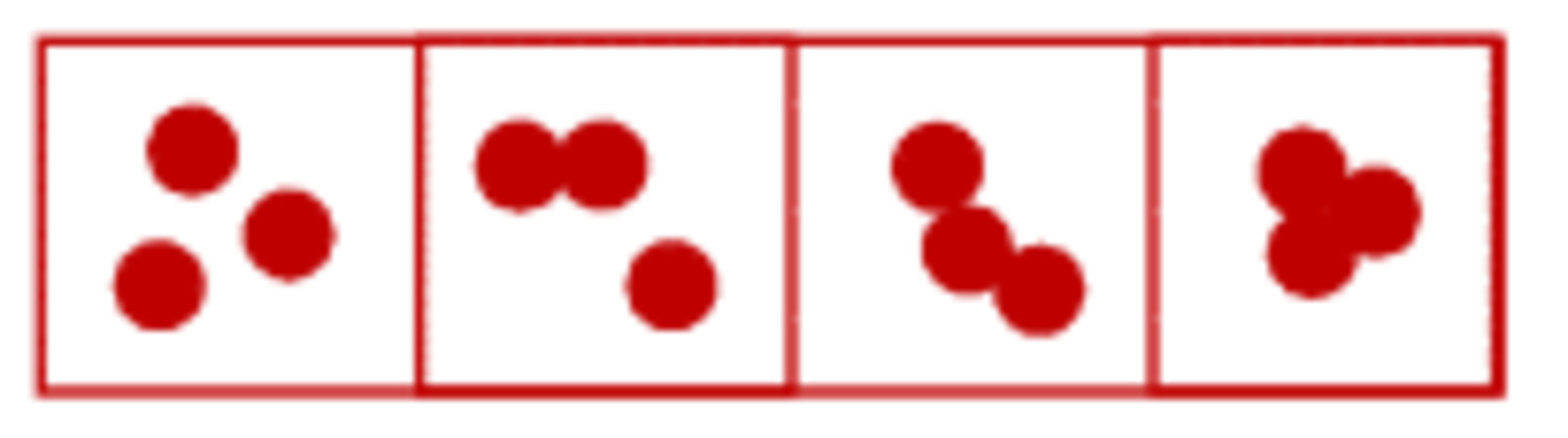
Five identical non-overlapping unit circles lay in the same plane. Some of them may be tangent to each other. Any arrangements which can be made identical by rotating or sliding the circles within the plane without either generating or breaking points of contact are considered to be the same configuration. How many different configurations are possible?

The image above shows the four different configurations available for three such circles.


The answer is 25.

Marta Reece by Marta Reece , 69, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Abel McElroy
Feb 23, 2017

0 Helpful 0 Interesting 0 Brilliant 0 Confused

1) High card
2) One pair
3) Two pair
4) Full house
5) Three of a kind
6) Four of a kind
7) Five of a kind (+ Joker) / Straight


Saya Suka - 2 months, 2 weeks ago
Marta Reece
Jan 16, 2017

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Playing devil's advocate, how do we know that's all there is?

I think that adding the graph interpretation of the diagrams would help make it clearer what scenarios arise.

Calvin Lin Staff - 4 years, 4 months ago

Log in to reply

Not that I have a proof, but this is apparently called 'penny graphs' with at least 2 connected sequences listed on OEIS, A085632 (for the connected one) and A085633 (for the total).

Saya Suka - 4 years, 4 months ago

I seemed to be able to find 40. It's possible I double-counted some by mistake, however. But right off the bat, I see one missing from your chart. In the fourth row, first column, you should have a counter part to that one that changes its handedness.

James Wilson - 3 years, 8 months ago

Log in to reply

No, the handedness is not an issue there. You can take the one with the bump on the right and twist it so that the head nods leftward and make the one with the bump on the left without anything disconnecting. There is only one there, the one with a tail of two dots connected to three dots in a triangle.

Marta Reece - 3 years, 8 months ago

Log in to reply

Aha! I see it now.

James Wilson - 3 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...