Maksimum

This is a pretty famous olympiad inequality problem, so let me present a classical inequality approach. There are actually several ways to tackle this, and this is my favorite (for reasons which you will see).

---

We will prove something stronger. For non-negative reals, we have
$27(x^2y+y^2z+z^2x + xyz) \leq 4 ( x + y + z) ^3$

Proof: WLOG, let $y$ be the middle number. Since $(y-x)(y-z) \leq 0$ , thus $y^2 + xz \leq xy + zy$ . Then,

$\begin{aligned} 27(x^2y+y^2z+z^2x + xyz) & = 27[ x^2y + xyz + z(y^2 + zx) ] \\ & \leq 27 ( x^2y + xyz + xyz + z^2y ) \\ & = 27 y ( x + z) ^ 2 \\ & = 4 \times 27 y \times \frac{x+z}{2} \times \frac{x+z}{2} \\ & \leq 4 \times ( y + \frac{x+z}{2} + \frac{x+z}{2} ) ^ 3 \\ & = 4 ( x + y + z) ^ 3 \\ \end{aligned}$

For equality to hold, we need $z(y-x)(y-z) = 0$ and $y = \frac{x+z}{2} = \frac{x+z}{2}$ .
This occurs when $x = y = z$ or when $z = 0 , x = 2y$ . $_\square$

---

Applying this to the problem,

$27(x^2y+y^2z+z^2x) \leq 27(x^2y+y^2z+z^2x + xyz) \leq 4 ( x + y + z) ^3$

We have equality when $z = 0, x = 2y$ (and cyclic permutations).

Write $f(x,y,z) = x^2y + y^2z + z^2x$ . In what follows, we assume that $x,y,z \ge 0$ and that $x+y+z=9$ . By symmetry, we can also assume that $x \ge y,z$ . Then $f(x,y,z) - f(x,z,y) \; = \; x^2y + y^2z + z^2x - x^2z - z^2y - y^2x \; = \; (y-z)(x^2 + yz - xy - xz) \; = \; (y-z)(x-y)(x-z)$ and so we see that $f(x,y,z) \ge f(x,z,y)$ for $x \ge y \ge z$ . Thus we see that $f(x,y,z)$ will be maximised when $x \ge y \ge z \ge 0$ . Since $f(x+z,y,0) - f(x,y,z) \; = \; (x+z)^2y - x^2y - y^2z - z^2x \; = \; 2xyz + yz^2 - y^2z - z^2x \; = \; yz(x-y) + xz(y-z) + yz^2 \ge 0$ for $x \ge y \ge z \ge 0$ , we see that $f(x,y,z)$ will be maximised when $x \ge y \ge z = 0$ . Thus we need to maximise $f(x,9-x,0) = x^2(9-x) \hspace{2cm} 4.5 \le x \le 9$ and this is maximised when $x=6$ , giving us a maximum value of $\boxed{108}$ .

I used Lagrange multipliers for this. This uses partial differentiation

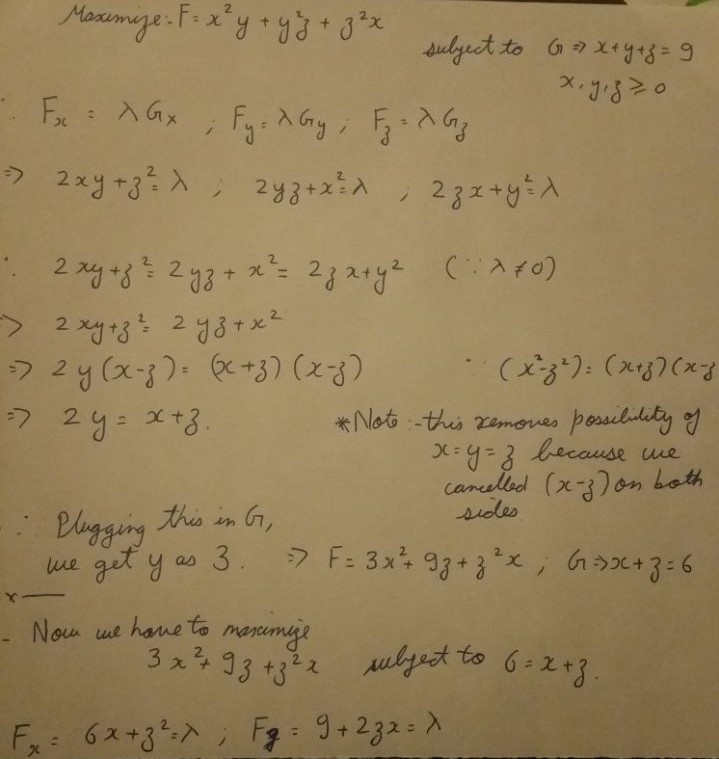
Don't hate me for using calculus to do an algebra problem

I am kind of suspicious of this approach though. Might need some corrections @Calvin Lin @Mark Hennings