Mama Geometry

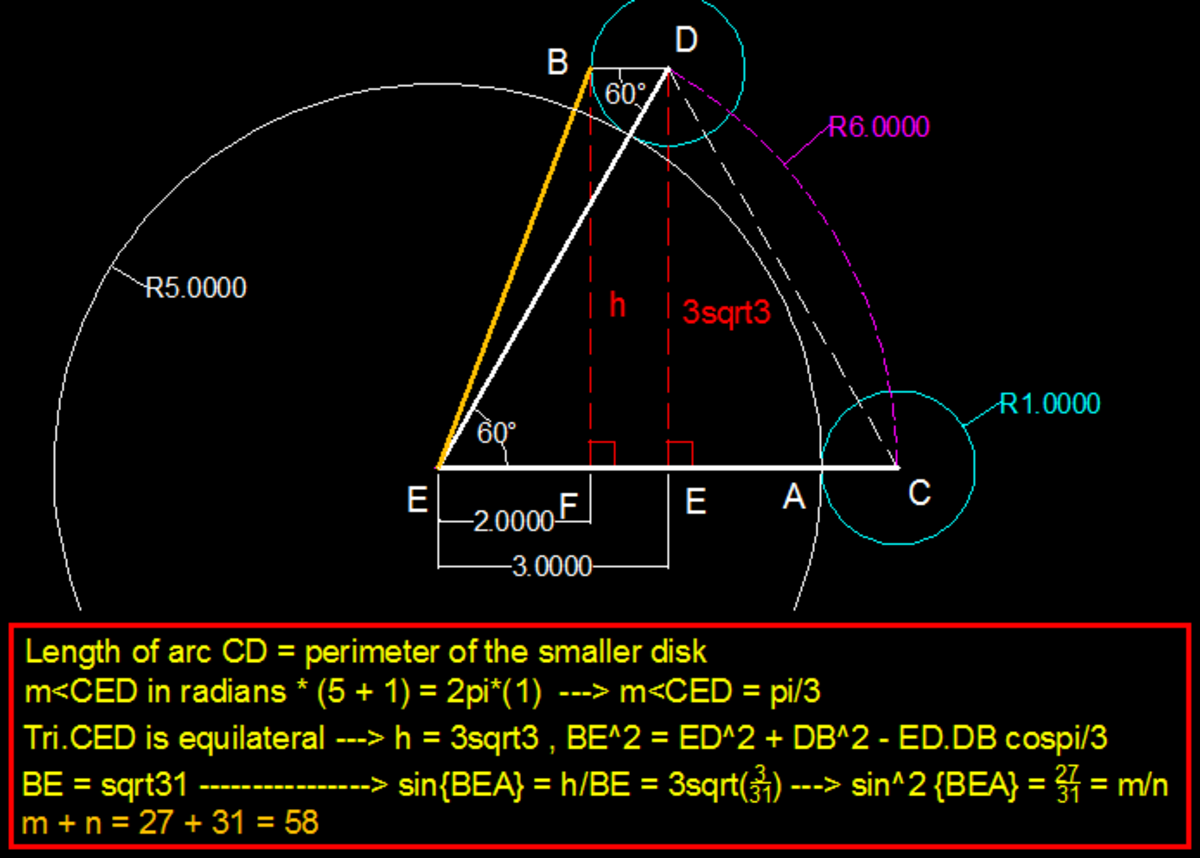
A disk with radius $1$ is externally tangent to a disk with radius $5$ . Let $A$ be the point where the disks are tangent, $C$ be the center of the smaller disk, and $E$ be the center of the larger disk. While the larger disk remains fixed, the smaller disk is allowed to roll along the outside of the larger disk until the smaller disk has turned through an angle of $360^\circ$ . That is, if the center of the smaller disk has moved to the point $D$ , and the point on the smaller disk that began at $A$ has now moved to point $B$ , then $\overline{AC}$ is parallel to $\overline{BD}$ . Then $\sin^2(\angle BEA)=\dfrac{m}{n}$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .