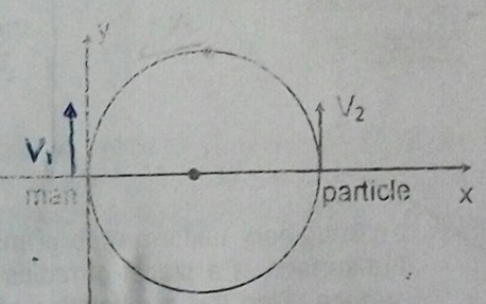
Man and particle

Classical Mechanics Level pending

A particle of mass m m moves with a uniform speed V 2 V_2 in a circle of radius R R , centered at ( R , 0 ) (R,0) in the x − y x-y plane. A person moves along the y y -axis with a uniform velocity V 1 V_1 . At t = 0 t= 0 , the man as well as the particle are located on the x x -axis and moving in the same direction. Find the angular momentum of this particle with respect to the man at the time t = π R 2 V 2 t = \dfrac{\pi R}{2V_2} .

[ m V 1 R ( 1 + π 2 ) − m V 2 R ] ( − k ^ ) \left [ mV_1 R \left(1 + \frac\pi2 \right) - mV_2 R \right ] (-\widehat k) m V 2 R ( − k ^ ) mV_2 R (-\widehat k ) [ m R ( π V 1 2 ) 2 + V 2 2 ] ( k ^ ) \left [ mR \sqrt{ \left( \frac {\pi V_1} 2 \right)^2 + V_2 ^2 } \right ] (\widehat k) m R ( π V 1 2 + V 2 ) ( + k ^ ) mR \left( \frac{\pi V_1}2 + V_2 \right) (+\widehat k)

Ayush Choubey by Ayush Choubey , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

0 solutions

No explanations have been posted yet. Check back later!

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...