Manipulating Dimensions

Algebra Level 1

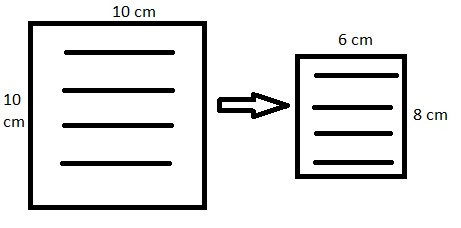
Harihar has written a research paper consisting of 10 pages on a Word file. The file only contains characters, without spaces. All the pages are completely filled by characters and there's no more space left at all. However, his advisor has asked him to write even more pages. Harihar does not want to write any more pages. However, he has a new trick up his sleeve : change the dimensions of the pages so that his text occupies more space. Currently, the dimensions of the pages are $(10 \times 10)$ $cm^{2}$ . Harihar reduces the length to 8 cm and the breadth to 6cm. Assuming that each character in the paper is square shaped of unit dimensions, how many pages will his research paper consist of after resizing the dimensions ?

20 21 22 23

2 solutions

Blan Morrison
Oct 6, 2018

Like the problem says, each character takes up $1~\text{cm}^2$ of space. If we assume there are no margins, that means Harihar has written exactly 1,000 ( $10(10\times 10)$ ) characters. The new page dimensions will contain $6\times 8=\boxed{48}$ characters. Therefore, if we distribute all 1,000 characters over $p$ pages containing 48 characters, we get $\left\lceil \frac{1,000}{p}\right\rceil=48$ $\implies p=\left\lfloor\frac{1,000}{48}\right\rfloor=\boxed{21}$

Mohit Kumar Basak
Oct 6, 2018

I believe that the problem is simple.

The number of characters remains unchanged while changing the dimensions.

Hence, total number of characters = characters in one page * Number of pages

Since characters have unit dimensions,

Total number of characters in one page = 10*10=100

Total characters = 10*100 = 1000

Now, in the new page, total number of characters in one page = 6 * 8 = 48

Hence, total pages required = 1000 / 48 = 20.8333333333

Since there are decimal digits, it means that one extra page is required, which gets partially filled with characters.

Hence, the answer is 21.

Manipulating Dimensions

2 solutions

0 pending reports