Manipulating Exponent
3 x 2 2 0 1 5 y x y = = = 2 2 0 1 5 8 1 ?
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
Awesome solution!
Can it be solve like that!!!!!!!!!!!!!!! 4 3^x=2^2015 2^2015y=81 (2^2015)^y=81 (3^x)^y=3^4 3^xy=3^4 xy=4
nice solution
3^^x=2^^2015 implies x=2015log(2)/Log(3) 2^^2015y=81 implies y=4 log(3)/2015 log(2) so xy=2015 log(2) * 4log(3)/log(3)*2015 log(2) after cancelling out terms XY becomes 4
3= 2^2015 /3^x-1, 3= 2^2015y/3^3, Thus by Cross Multiplication 3^3 * 2^2015= 3^(x-1) * 2^2015y, Thus If x-1=3, x=4 and y=1, Thus xy=4
I can definitely see it. It is perfect
3^x=2^2015 and 2^2015y=81.So 3^xy=81,3^xy=3^4 so xy=4
We have to take natural log in both these equations 3^x = 2^2015 & 2^2015y = 81
ln3^x = ln 2^2015
xln3 = 2015 ln2
x = 2015 ln2/ln3
ln 2^2015y = ln 81
2015yln2 = ln 81
y = ln 81/2015 ln 2
Now xy = [2015ln2/ln3 ] * [ln81/2015ln2 ]
Now the 2015 ln 2 gets cancelled out so we are left with
xy= ln81/ln3 = 4
As 3^x = 2^2015, Multiply powers with y we get 3^xy = 2^2015y Implies from 2nd eq 3^xy =81 = 3^4 which implies xy = 4
3^x = 2^2015 2^(2015y) = 81 3^(xy) =81 xy=4
Because my lucky number is four
2^2015y = 3^xy 81 = 3⁴ Hence xy = 4
Taking log both sides of both equation and then simply simplifying... Xlog3 = 2015log2 , 2015ylog2 = 4log3. , we get xy = 4
x=2015(log2)base3. y=4/2015(log3)base2. multiplying. (log2)base3 (log3)base2=1.(log property); so x y=4...
3 POWER 4 (3^4)= 2 POWER 2015 Y, 3 POWER x (3^x)=2 POWER 2015 , SO X=4,Y=1 X Y=4 1=4
3^4= 2^(2015y), 3^x=2^(2015); 3=2^(2015y/4), 3=2^(2015/x); 2015y/4=2015/x; y/4=1/x xy=4
3^x = 2^2015
(3^x)^y = (2^2015)^y
3^xy = 2^2015y = 81 = 3^4
xy = 4
its a matter of understanding properties of exponents. Substitute 3^X to 2^2015 in in 2nd equation. making it 3^xy = 81. then 3^xy = 3^4....therefore xy = 4......
3^x = 2^2015 2^2015y = 81 (y != 0, because 2^2015y = 81 => 1 = 81) (y != 1, because 2^2015 = 81 => 2^7 = 128, 128 > 81 => 2^2015 > 81 (2^x < 2^(x+1)) (2^2015)^y = 3^4 2^2015 = 3^(4/y) 3^x = 3^(4/y) x = 4/y xy = 4
Logarithm can be used too, but could be tedious
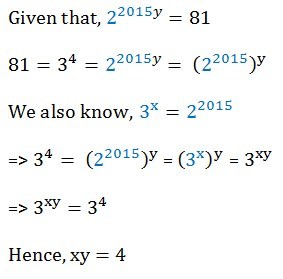

3 x = 2 2 0 1 5 = > 3 x y = 2 2 0 1 5 y
But, 2 2 0 1 5 y = 8 1
= > 3 x y = 8 1 = > 3 x y = 3 4 = > x y = 4