Manipulating Riemann's Zeta Function
Knowing that
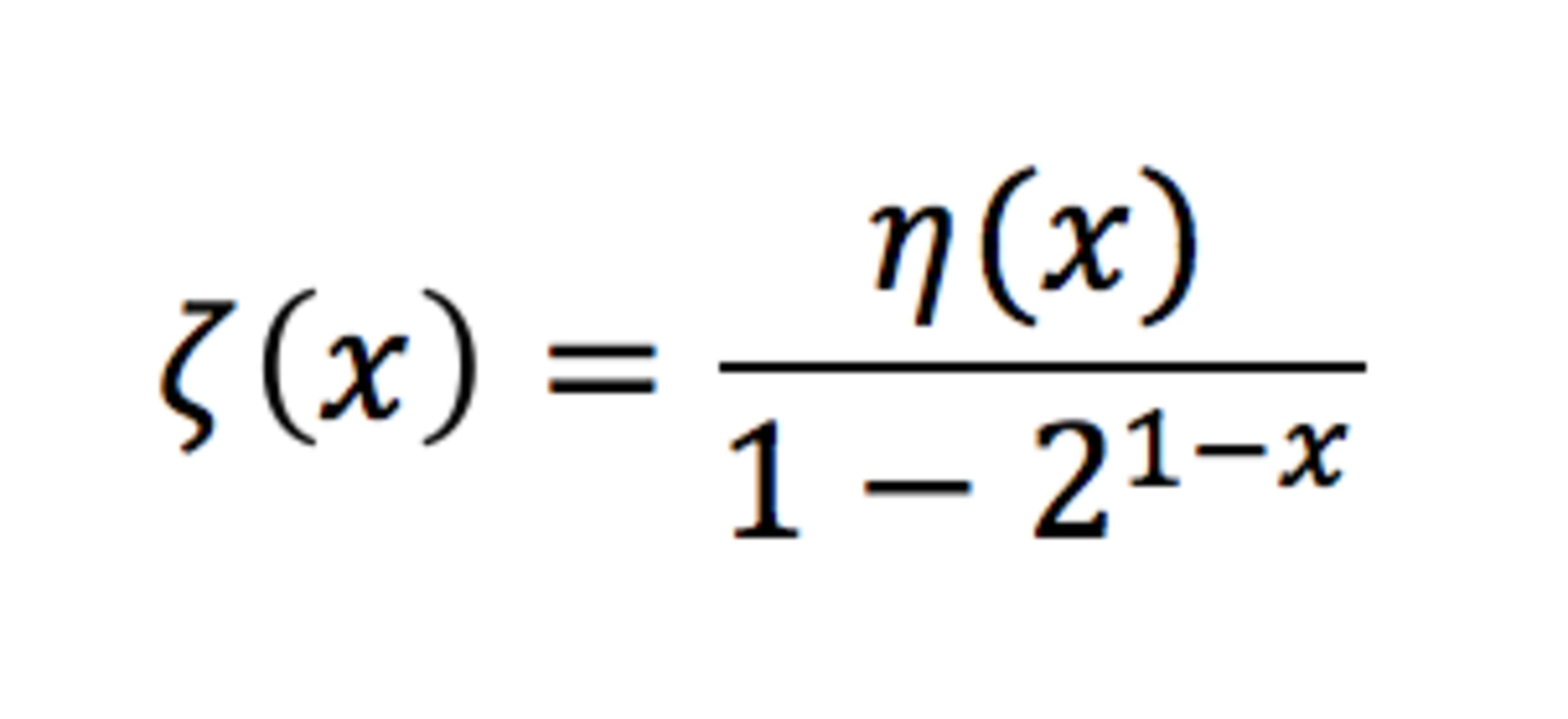and that
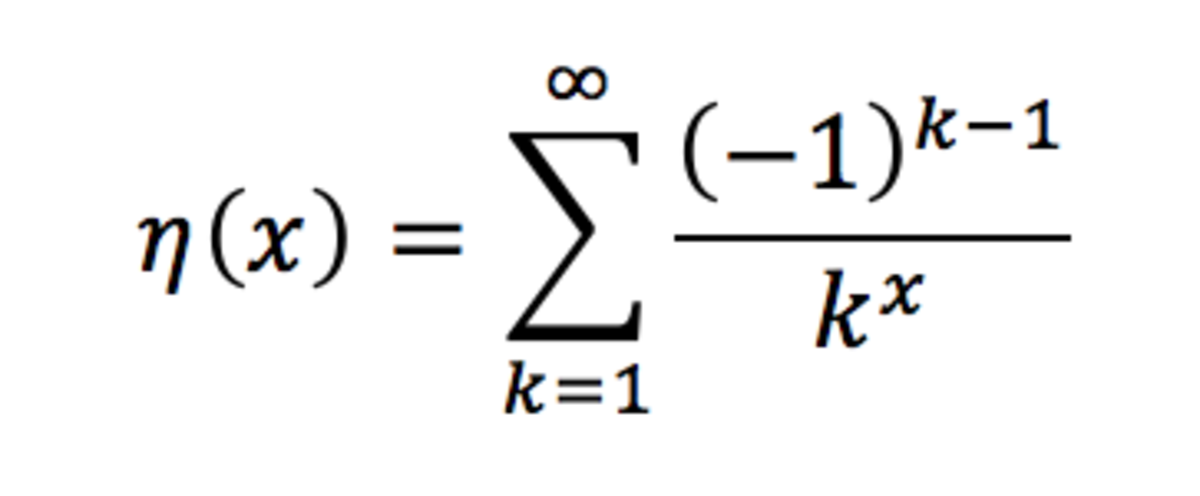, manipulate
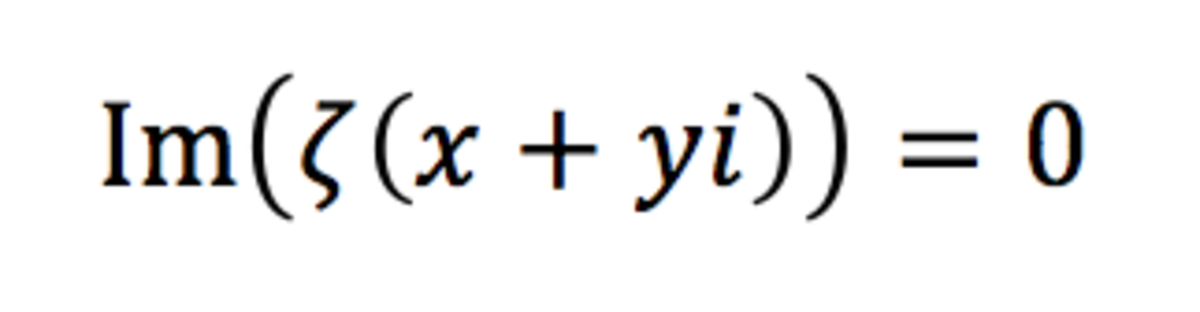so that is is expressed in an infinite sum that contains only the sigma sum operator and basic operations (addition, subtraction, multiplication, division and exponents).
A:
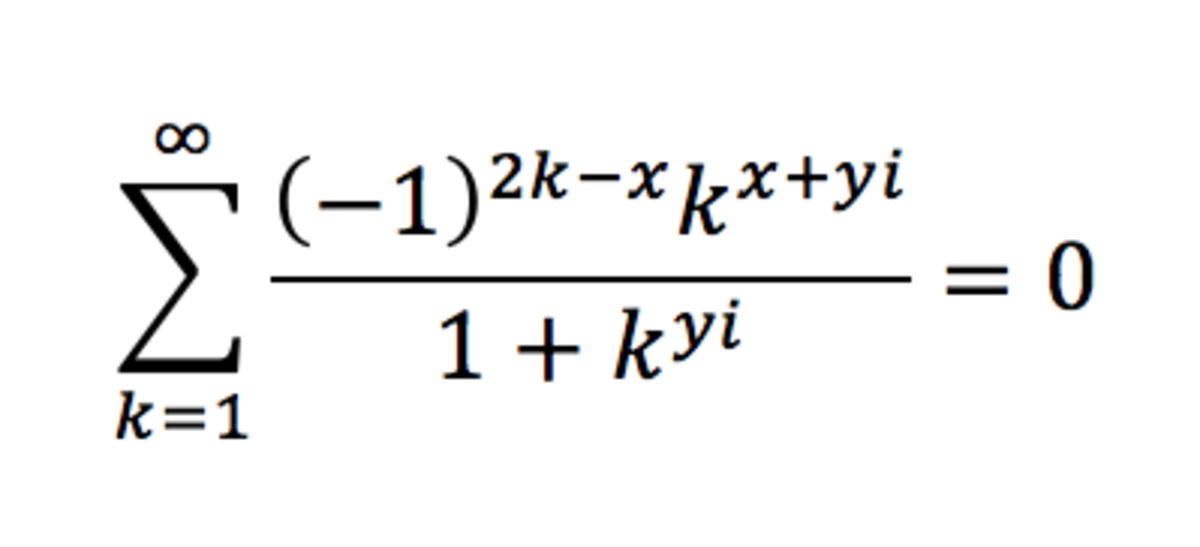
B:
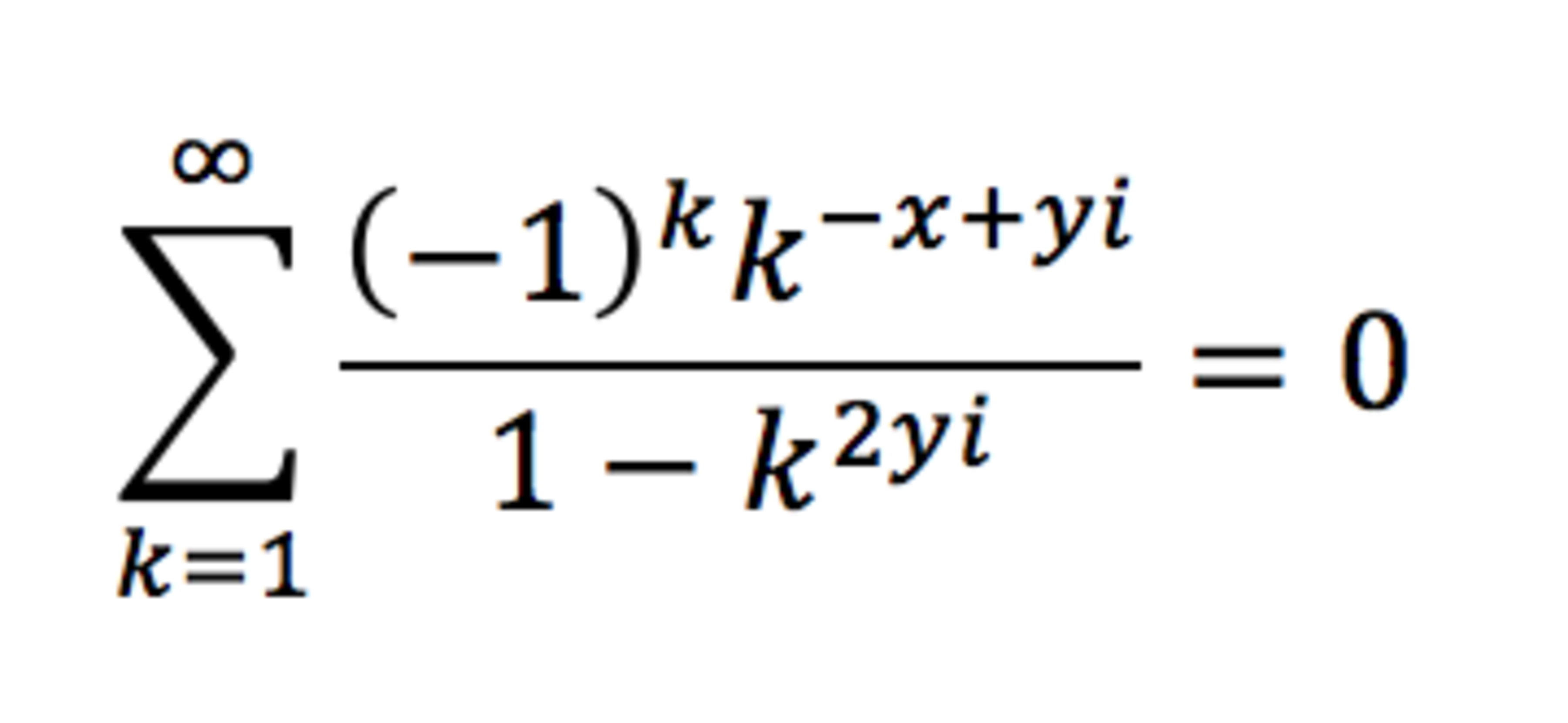
C:
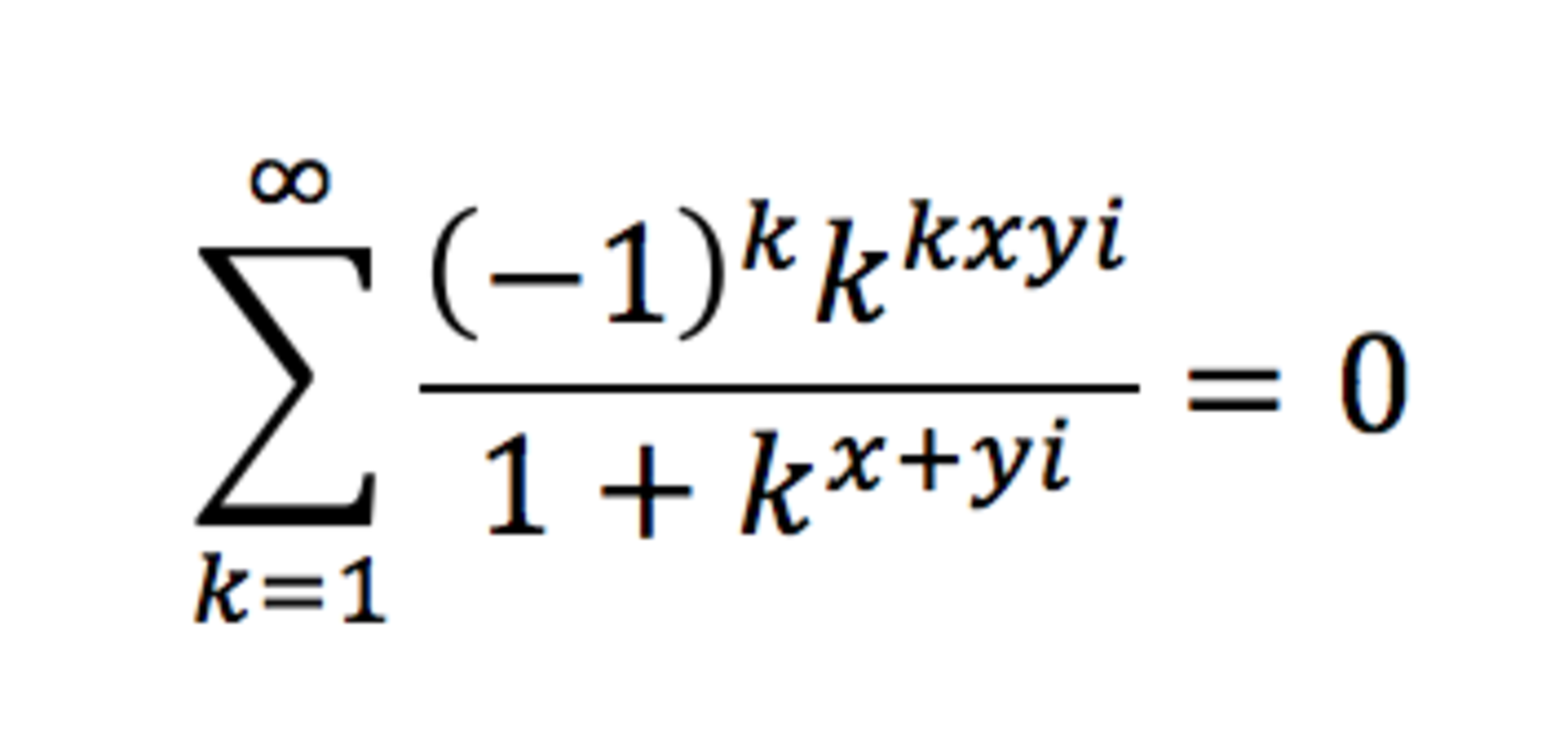
D:
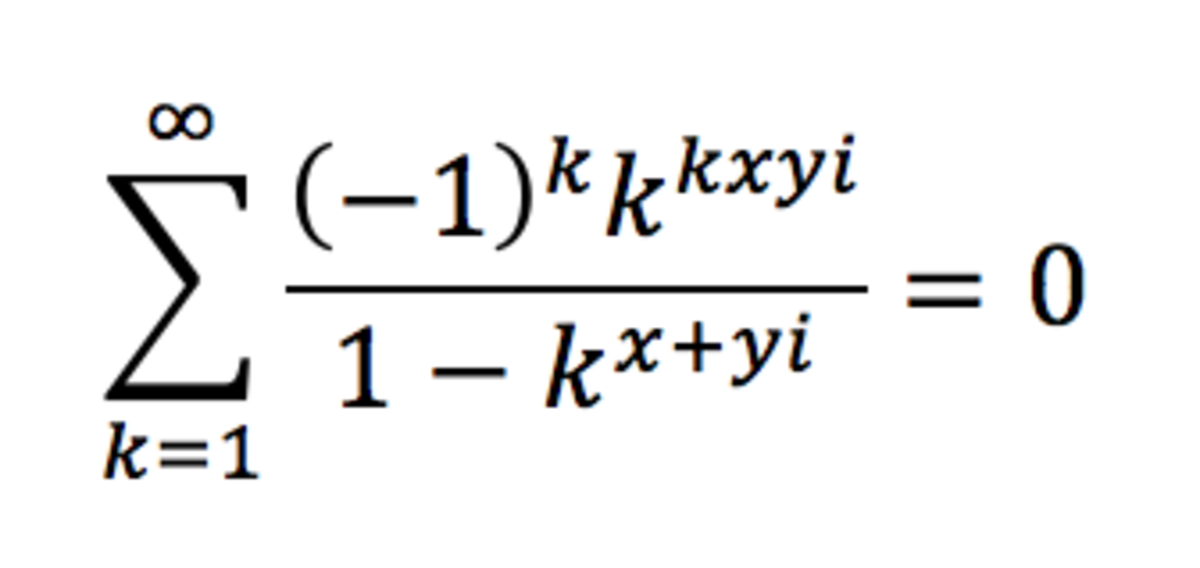
E:
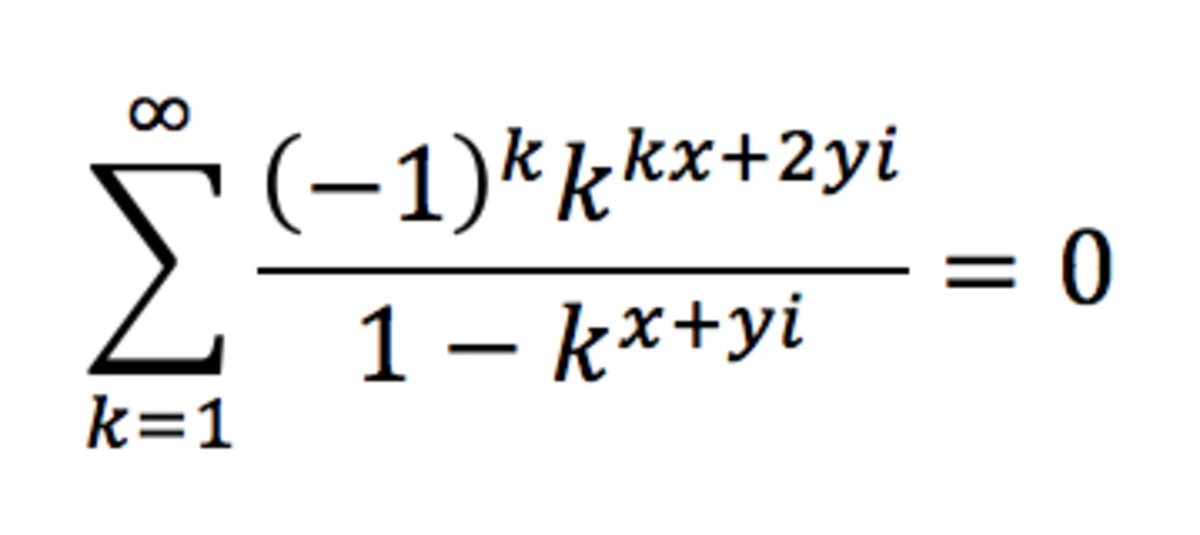
Note:
You can also try doing the same thing using the regular form of the zeta function or using the following equation.
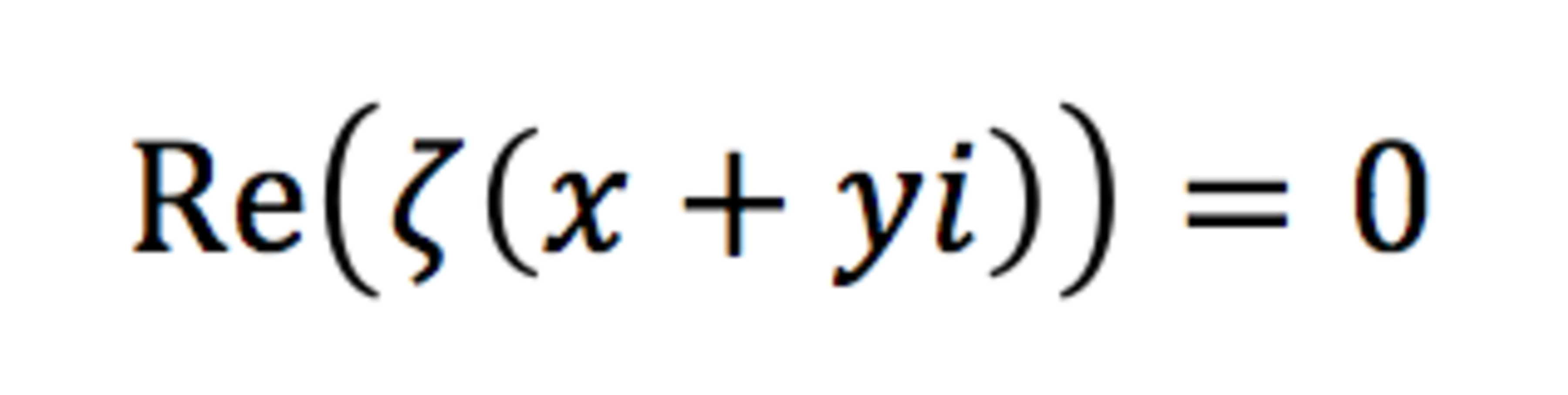
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
There is two ways two solve this problem; first you can just manipulate the equation, I encourage you to do it, this procedure will need some knowledge on the functions Im(x) and Re(x) which you can build up by studying them. The other way of proceeding is by deducing that all of the other choices are impossible responses. First C and D can be eliminated, because it is not very likely that kxyi will all get multiplied together, even less that the will be an exponent. Second, E can be eliminated for almost the same reason. Why would k be multiplied with x and not with yi ? Finally, in A having 2k-x as an exponent to -1 in impossible, because x was never an exponent of -1 in the first place. You are therefore left with B as the only option.