So Many Shapes!

Relevant wiki: Regular Polygons - Problem Solving - Medium

Nice problem! I think this is a really great example of a problem that a lot of people get right because intuition lines up with reality. Intuition says that spheres and circles are the most efficient ways to contain volume and area respectively. Think about soap bubbles - the surface area of a soap bubble is trying to shrink as much as it can given how much air is trapped inside. And the shape that the bubble makes when executing this optimization is an almost-perfect sphere. Thinking about circles in this light, as the "super-efficient" shape, intuition might then suggest that shapes with a lot of sides are more like circles. Basically, you might guess that the triangle might be the least efficient area-holder if the circle is the most efficient area-holder.

But let's do better than guess. This is intuition is pretty strong, but it is not a proof. And this problem can be solved, rigorously, without any trigonometry or anything fancy. Here is a proof of what your intuition's trying to tell you:

Facts

1) The square contains less area than the octagon.

Proof: If the side length of the square is $S$ , then the area of the square is $S^2$ and the side-length of the octagon is $\frac{S}{2}$ . Consider the following shape inscribed within the octagon:

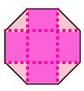
The area of the small central square is $(\frac{S}{2})^2 = \frac{S^2}{4} = D$ . The area of two of the rectangles to the sides of that small square, put together, must be strictly larger than $(\frac{S^2}{2})^2$ because the short side length of each rectangle must be greater than $\frac{S}{4}$ by the triangle inequality, we'll call the area of all 4 rectangles together $2D+x$ . And the 4 light pink triangles are all right triangles and can be fit together into another $(\frac{S^2}{2})^2 = D$ square, bringing the total area to $4D + x = 4\times \frac{S^2}{4}+x= S^2 + x$ .

2) The triangle contains less area than the hexagon

Proof: again we start by noting that if the side length of the triangle is $S$ , then the side-length of the hexagon is $\frac{S}{2}$ . This means that the triangle is made out of 4 side-length- $\frac{S}{2}$ equilateral triangles, whereas the hexagon is made out of 6 of the same triangles. Therefore, the hexagon is much bigger than the triangle.

3) The triangle contains less area than the square and less area than the circle

Proof: let's just do this set via area formulas. Say that the total perimeter is P.
a. The area of an equilateral triangle with side length $\frac{P}{3} = \frac{\sqrt{3}}{4} (\frac{P}{3})^2= \frac{\sqrt{3}}{4(9)} P^2 = ~.048P^2$
b. The area of a square with side length $\frac{P}{4} = (\frac{P}{4}) ^2 =.0625P^2$
c. The circumference of the circle is $2 \pi r = P$ , so $r = \frac{P}{2 \pi}$ . Therefore, the area of the circle is $\pi r^2 = \pi (\frac{P}{2 \pi})^2 = \frac{1}{4 \pi}P^2 = ~.0796 P^2$ .

Therefore, the triangle has the smallest area of all of the shapes above!

Let 3 units be the perimeter. So $2\pi*r=3 \ and \ area \ =\dfrac{1.5^2}{\pi}=.716....\text{For an infinite sided circle}\\ Area \ of \ \Delta=\dfrac{\sqrt3}4=.433...\\ \text{So as we increase the sides area goes on increasing.}$