Many functions
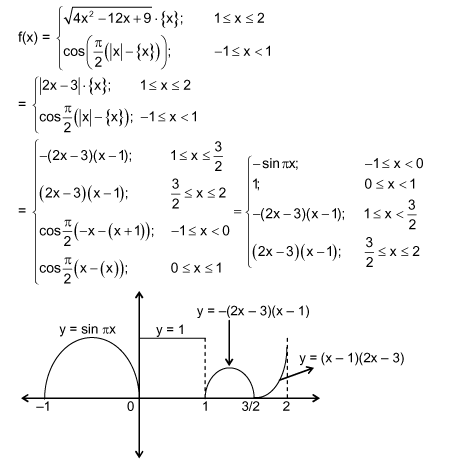
f ( x ) = ⎩ ⎨ ⎧ { x } ⋅ 4 x 2 − 1 2 x + 9 , cos ( 2 π ( ∣ x ∣ − { x } ) ) , 1 ≤ x ≤ 2 − 1 ≤ x < 1
Consider the piecewise function f ( x ) above with { x } denoting the fractional part of x .
Which of the following is/are true?
A . Range of f ( x ) = [ 0 , 1 ]
B . The number of values of x for which function is continuous but not differentiable is 1 .
C . f ( x ) = 1 has two solutions.
D . Number of values of x for which f ( x ) is discontinuous is 2 .
Try my set .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Tanishq Varshney Look's like ABD seems to do well in math as well :P (ABD = Ab De Villiers )
There are three points of discontinuity, namely at x = 0 , 1, and 2, so D is not true.
Log in to reply
well , what i have learnt says that till u dont know the curve for a value a, u cant consider the function discontinuous, I mean to say for x ≤ 2 we know the curve but not for x > 2 . Hence we cant say its discontinuous at 2 same goes for − 1 . Plz correct me if i am wrong
Log in to reply
f ( 2 ) = 0 , but x → 2 − lim f ( x ) = 1 , so f ( x ) is not continuous at x = 2 .
I agree with @Jon Haussmann sir. The function becomes 0 at x=2 whereas its left hand limit is 1. so it is discontinuous at x=2.
sir just then one doubt why did u first mark ABD as correct although i provided the none of these option