Many Points, Many Segments

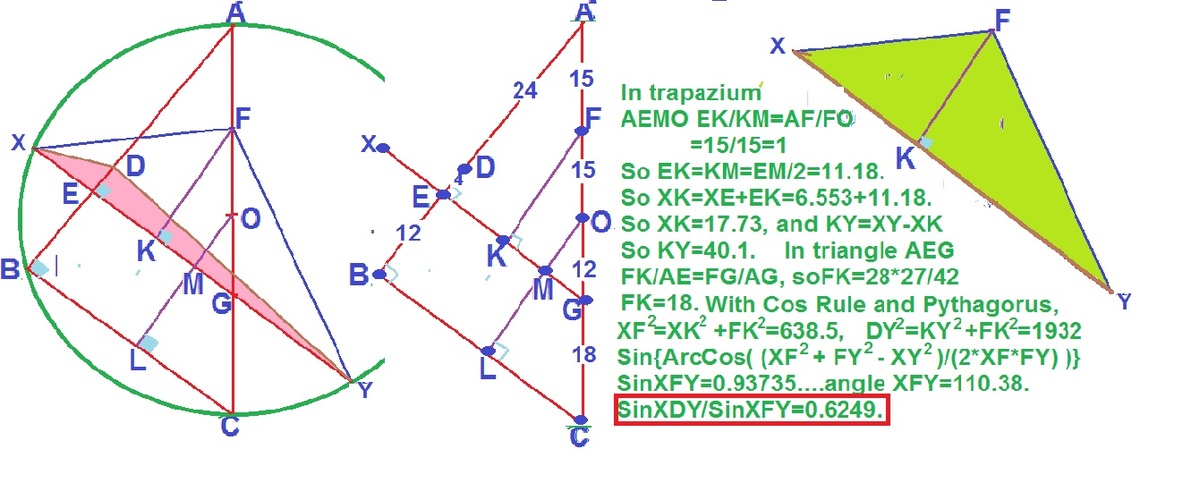
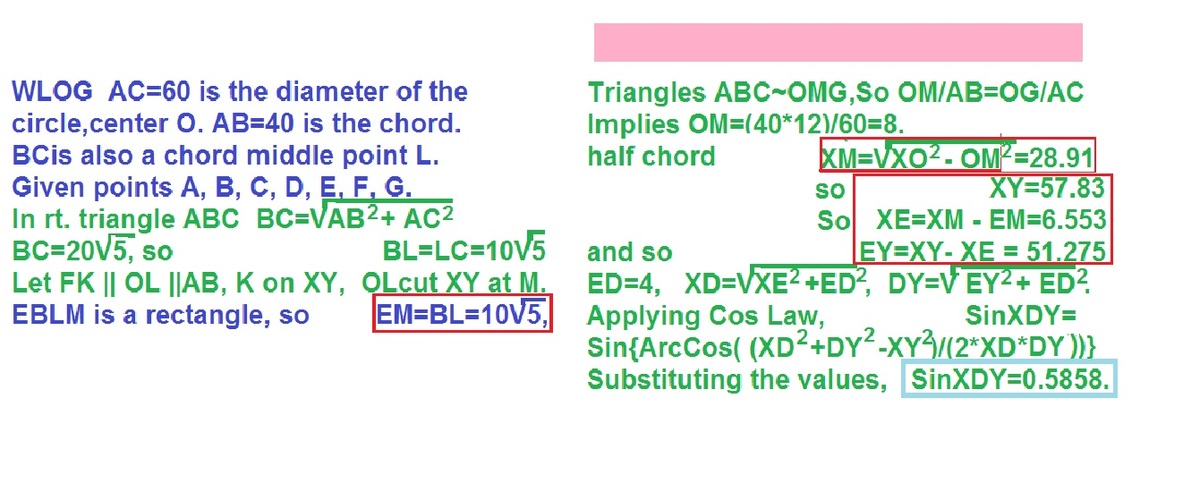
This problem has many geometrically significant points in disguise, I will expose them now: $D,F$ are isogonal conjugates wrt $\triangle AXY$ . This will follow from an important property about isogonal conjugates below:

---

Property1: Suppose $P,Q$ are isogonal conjugates wrt $\triangle ABC$ . Let $AP$ meet $BC,(ABC)$ at $A_P, P_A$ respectively; define $A_Q, Q_A$ similarly. For simplicity reasons assume $P,Q$ lie inside the triangle. Prove that $\frac {PA_P}{A_PP_A}=\frac {AQ}{QQ_A}$ and (symmetrically) $\frac {QA_Q}{A_QQ_A}=\frac {AP}{PP_A}$

Proof: Angle chasing gives: $\angle PBP_A=\angle PBA_P+\angle P_ABA_P=\angle ABQ+\angle BAQ_A=\angle BQQ_A$ . Since $\angle AQ_AB=\angle AP_AB$ , therefore $QBQ_A\sim BPP_A$ .

Define $T$ on $BQ_A$ such that $QT||AB$ , then $\angle BQT=\angle ABQ=\angle PBQ\implies$ $QBQ_A\cup T\sim BPP_A\cup A_P\implies \frac {PA_P}{A_PP_A}=\frac {BT}{Q_AT}=\frac {AQ}{QQ_A}$ . The second ratio equality follows analogously. $\Box$

---

Now we show that $D,F$ are isogonal conjugates wrt $\triangle AXY$ . We will designate $X,E,G,Y$ to be collinear in that order:

Notice that $\frac {BE}{CG}=\frac {2}{3}=\frac {AB}{AC}$ , therefore $EG||BC||XY$ . It follows that cyclic $XYCB$ must be an isosceles trapezoid and thus $XB=CY\implies \angle XAB=\angle CAY$ or that $AB,AC$ are isogonal wrt $\angle XAY$ .

Let $F'$ denote the isogonal conjugate of $D$ wrt $AXY$ , then $F'$ lies on $AC$ . By Property 1, $F'$ satisfies: $\frac {AF'}{CF'}=\frac {DE}{BE}=\frac {1}{3}$ This, of course, fits the description of $F$ as $\frac {AF}{CF}=\frac {15}{45}$ , therefore $F=F'$ and we have proven our claim.

To find $\frac {\sin \angle XDY}{\sin \angle XFY}$ , we have to use another property of isogonal conjugates:

---

Property2: In the same set up as property 1, prove that $\frac {\sin \angle BPC}{\sin \angle BQC}=\frac {AQ}{AP}$ .

I will omit the proof for this as it is just a straightforward application of the triangle Sine law; there exists a more elegant solution that involves similarity.

---

Applying this property to our problem, the answer is $\frac {\sin \angle XDY}{\sin \angle XFY}=\frac {AF}{AD}=\frac {5}{8}=\boxed {0.625}$