Many ways to go
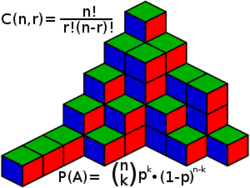
There are 10 people who are sitting in a round table. Two of them do not want to sit together. What are the number if ways in which they don't sit together?
The answer is 282240.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Total number of ways in which all 10 people can sit; (10-1)! = 9! Let's fix Bob and Bill's positions to be opposite each other. Rest 8 can sit in 8! ways. Now, BOB and Bill toggle their position; rest 8 will rearrange themselves in 8! way again.
Bob and Bill don't sit at the opposite tables = 9!-2x8! = 362880-2*40320=282240