Markov Chain Vocab

Probability Level 2

The graphs of two time-homogeneous Markov chains are shown below.

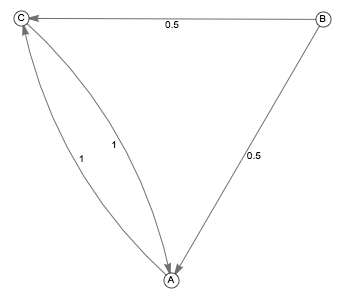Chain 1 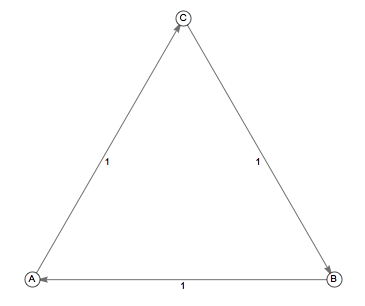Chain 1 Chain 2 Chain 2

Determine facts about their periodicity and reducibility.

Neither Markov chain is irreducible. Chain 1 is not irreducible, and chain 2 is not aperiodic. Chain 1 is aperiodic and irreducible, and chain 2 is aperiodic. Chain 1 is aperiodic, and chain 2 is irreducible. Both Markov chains are periodic and irreducible.

View wiki
Henry Maltby by Henry Maltby , 26, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Henry Maltby
Apr 28, 2016

Relevant wiki: Markov Chains

In Markov Chain 1, there is no way to get from state A (or C) to state B. Any move from state A (or C) to itself must take an even number of steps, so that state is periodic. Thus, Chain 1 is not irreducible and not aperiodic.

In Markov Chain 2, there is a way to get from any given state to any other. Any move from state A (or B, or C) to itself must take a number of steps divisible by 3, so that state is periodic. Thus, Chain 1 is irreducible and not aperiodic.

20 Helpful 2 Interesting 0 Brilliant 3 Confused

how come irreducible?

Raj Miglani - 4 years, 4 months ago

Log in to reply

See My answer

Anshul ujlayan - 2 years, 10 months ago

Is it possible to have a chain with states that are both aperiodic and periodic? If so, how would you classify the Markov Chain?

Brandon Buesching - 4 years, 3 months ago

In Markov Chain 1, how would we describe the "periodicity" of state B? Since there is no way to go from state B to itself, would we say that B has no period? Is B non-periodic?

Tyler Neisinger - 4 years ago
Anshul Ujlayan
Jul 30, 2018

The First Markov chain does not allow to transition to state B from state A or C though it all probability are postive, that's mean it's not irreducible. It also taking more than 1 steps from transiting from state A to State C or state C to State A, so it can not be aperiodic. So it periodic Markov Chain.

In Markov chain two, it's possible to transition from one state to other with three move and positive probability, so it's not aperiodic and irreducible.

4 Helpful 0 Interesting 0 Brilliant 3 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...