Mass and Wedge
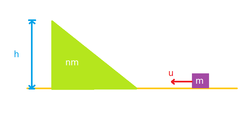 A block of mass
is pushed towards a movable wedge of mass
and height
. You may assume all the surfaces to be smooth. The minimum value of the velocity
with which the block
must be projected so that it would reach the top of the wedge is
A block of mass
is pushed towards a movable wedge of mass
and height
. You may assume all the surfaces to be smooth. The minimum value of the velocity
with which the block
must be projected so that it would reach the top of the wedge is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The wedge is movable so use momentum conservation to find the combined velocity of wedge + mass system.
Then use energy conservation for the system.