Mass on pulley

Classical Mechanics Level 2

A square mass $M_1$ of side length $2\text{m}$ is placed on a surface with gradient $\frac{1}{\sqrt{3}}$ . A rectangular mass $M_2$ is hung from a pulley which the cable attached to $M_1$ wraps around. The mass density of $M_2$ is $\rho(x,y)=c(x^2+y^2+xy)$ . If the minimum value of $c$ required for $M_2$ to drop is $c=\frac{A}{B}(C+\frac{\sqrt{D}}{E})$ , where $A$ and $B$ are positive, coprime integers and $D$ and $E$ are prime, enter $B-(A+C+D+E)$ .

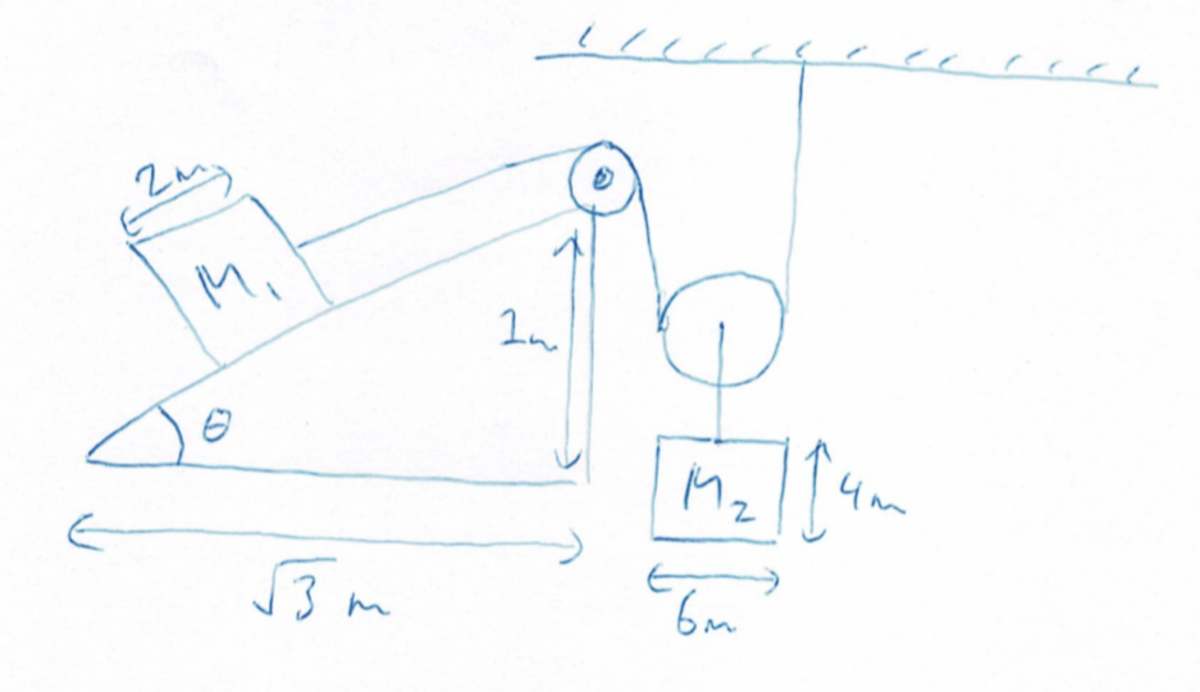
Details and Assumptions:

The coefficient of friction for the surface is $\mu=0.5$ .
$M_2$ has dimensions $\text{length}\times\text{width}=6\text{m}\times 4\text{m}$ .
The cable going out from the wheel with $M_2$ is meant to be entirely vertical.
For $M_2$ , treat the center of the rectangle as the origin.
$M_1$ has a uniform mass density of $5\text{kg/m}^2$ .

The answer is 15.

1 solution

Karan Chatrath
Apr 15, 2020

Nice problem.

Let the mass $M_2$ be calculated as such:

$M_2 = c\int_{-3}^{3} \int_{-2}^{2} \left(x^2 +y^2 +xy\right)dy \ dx$ $M_2 = 104c$

The mass $M_1$ is simply $M_1 = 20$ . Let the tension on the string be $T$ . Forming the equilibrium equations when the system is at rest and when the mass $M_2$ is just about to drop is:

$M_1g\left(\sin{\theta} + \mu \cos{\theta}\right) = T$ $2T = M_2g$

$\implies 2M_1 \left(\sin{\theta} + \mu \cos{\theta}\right)=104c \implies \boxed{c = \frac{5}{26}\left(1 + \frac{\sqrt{3}}{2}\right)}$

I have assumed the inclined surface to be fixed on the ground.

Oops I forgot that $1$ was not prime :/ stupid me

Charley Shi - 1 year, 1 month ago

Mass on pulley

The answer is 15.

1 solution

0 pending reports