Match Stick Squares
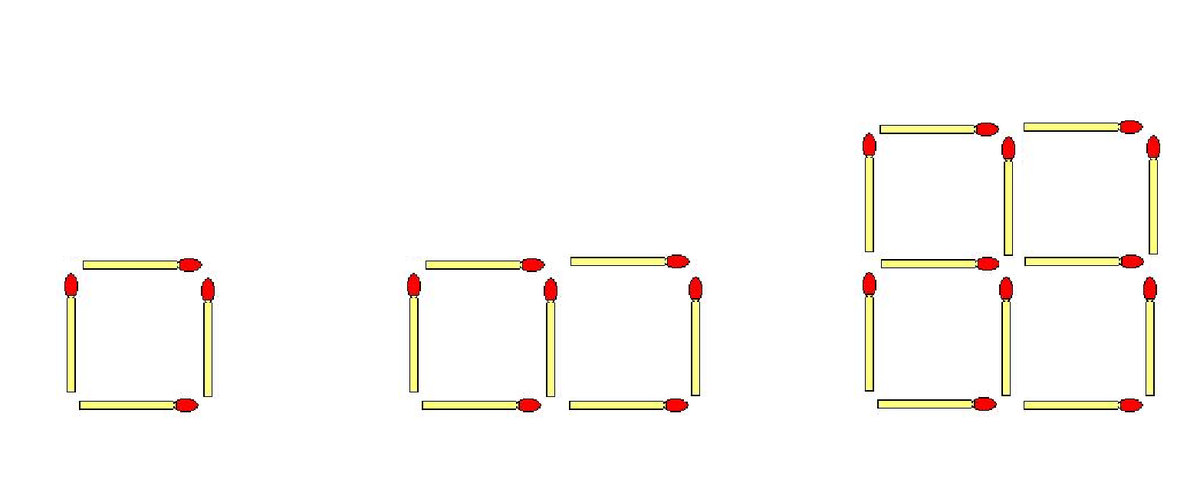
You are arranging match sticks to form a grid area for some rectangle. For example, a square unit has 4 match sticks; a rectangle of has 7 match sticks; and a square of has 12 match sticks, as shown above.
Then a square of is created with the same method before it is rearranged into a rectangle with the integer side lengths, by using the same amount of match sticks as the square.
What is the least possible area difference between the square and the new rectangle?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For a square of side length 1 7 , we can first calculate the total number of match sticks used:
For the vertical grids, we need 1 7 × ( 1 7 + 1 = 306) match sticks. Similarly, the horizontal grids will also yield the same amount.
Therefore, there are totally 6 1 2 match sticks used.
Suppose then that the new rectangle has side of a and b . The total amount of match sticks used can be evaluated as:
6 1 2 = b ( a + 1 ) + a ( b + 1 ) = 2 a b + a + b
Then let's generalize the formula for square of side x and let a = x − c and b = x + d for some positive integers c and d .
Hence, 2 x ( x + 1 ) = 2 ( x − c ) ( x + d ) + ( x − c ) + ( x + d ) .
0 = 2 ( d − c ) x − 2 c d + ( d − c )
2 x = d − c 2 c d − 1
Substitute x = 1 7 , we will get: 3 5 ( d − c ) = 2 c d .
Since 3 5 is odd, d − c is even.
Then let d − c = 2 k for some integer k .
3 5 ( 2 k ) = 2 c ( c + 2 k )
3 5 k = c ( c + 2 k )
0 = c 2 + ( 2 k ) c − 3 5 k
Solving for c , we will get: c = 2 − 2 k ± 4 k 2 + 4 ⋅ 3 5 k = − k ± k 2 + 3 5 k .
Since c is an integer, the square root residue must also be an integer.
In order to maximize the area, the side difference must be as minimal as possible. Then k = 1 applies.
Therefore, c = 5 and d = 7 : 3 5 × 2 = 2 × 5 × 7 .
As a result, a = x − 5 = 1 7 − 5 = 1 2 and b = x + 7 = 1 7 + 7 = 2 4 .
Checking the answer: 6 1 2 = 2 a b + a + b = 2 × 1 2 × 2 4 + 1 2 + 2 4 = 5 7 6 + 3 6 , which is correct.
As a result, the square will have an area of 1 7 × 1 7 = 2 8 9 , and the rectangle will have an area of 1 2 × 2 4 = 2 8 8 .
Thus, the area difference is 2 8 9 − 2 8 8 = 1 .