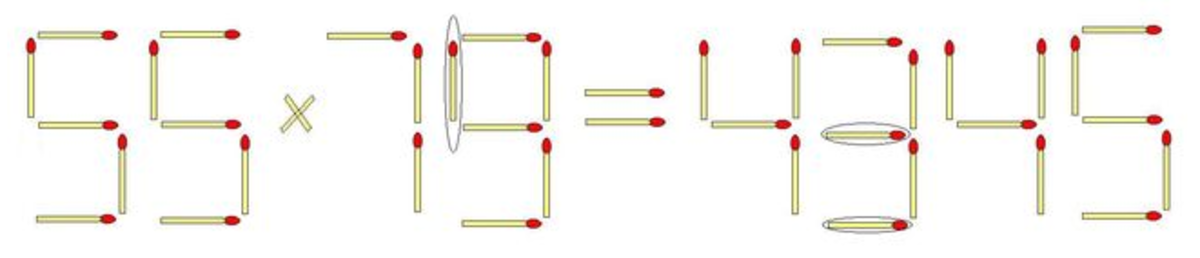
Match Sticks Mystery
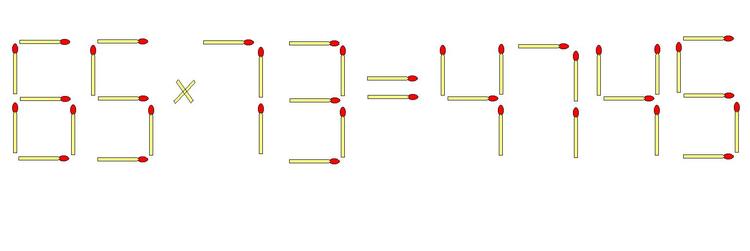 The match sticks are arranged so that the above equation is true.
The match sticks are arranged so that the above equation is true.
If you're allowed to move 1 match stick on the left and add 2 new matches to the right so that the edited equation is still true, what will the value of the new right-hand-side?
Please use the match sticks as the digital numbers below:
The answer is 4345.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
while the other solution is correct, i will show u how to think this through
if you add any 2 or 1 matches to four, it can become only 9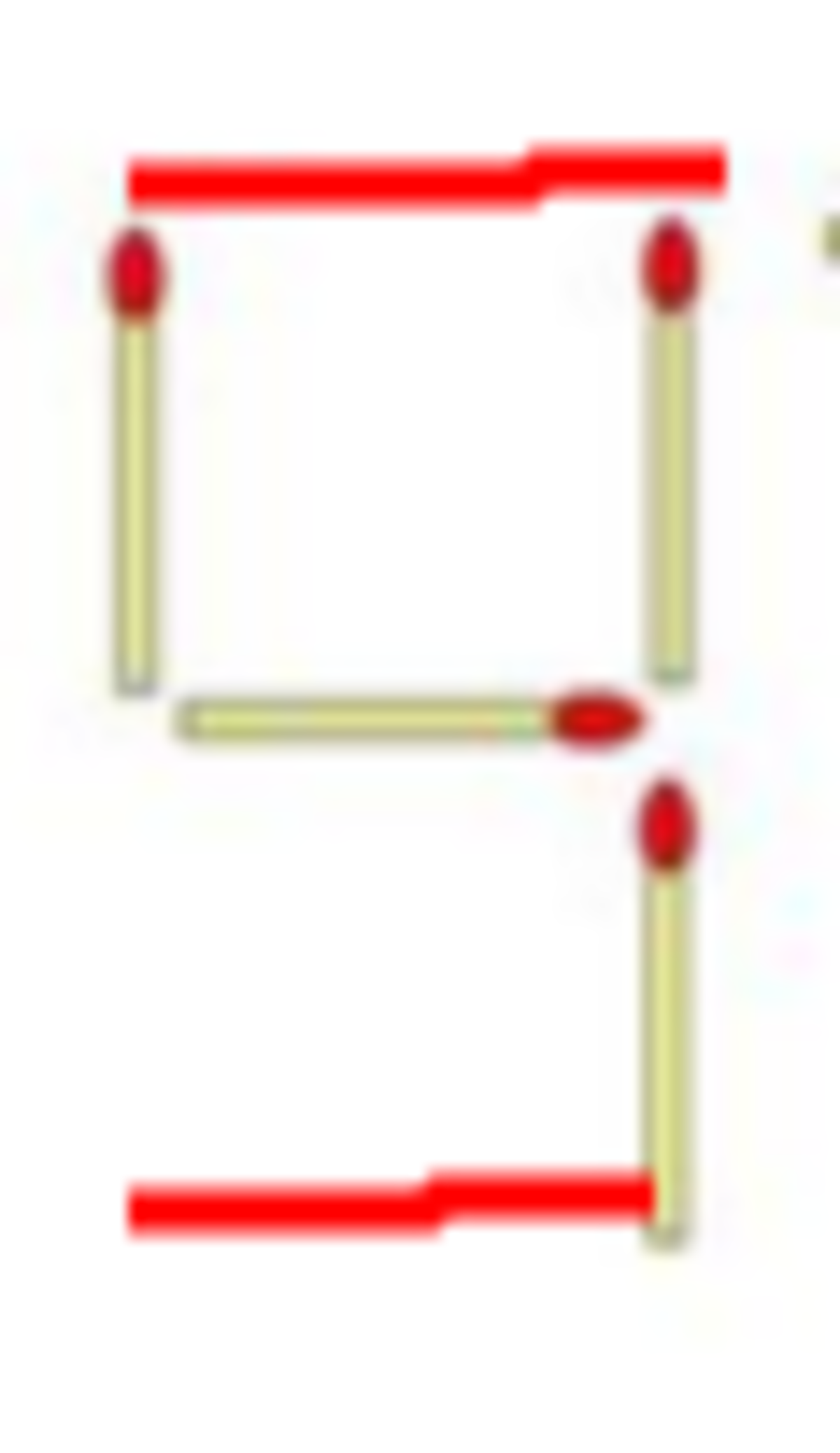 . so we look at the cases and see that moving 1 stick in the LHS will never make it big enough for nine and hence, the leading digit remains a 4.
now look at 5 in the LHS. does it have capability to lose a match. no! we move on to 7. it can lose its top to become a one
. so we look at the cases and see that moving 1 stick in the LHS will never make it big enough for nine and hence, the leading digit remains a 4.
now look at 5 in the LHS. does it have capability to lose a match. no! we move on to 7. it can lose its top to become a one
 , but then the maximum possible product would be
8
5
×
1
3
=
1
1
0
5
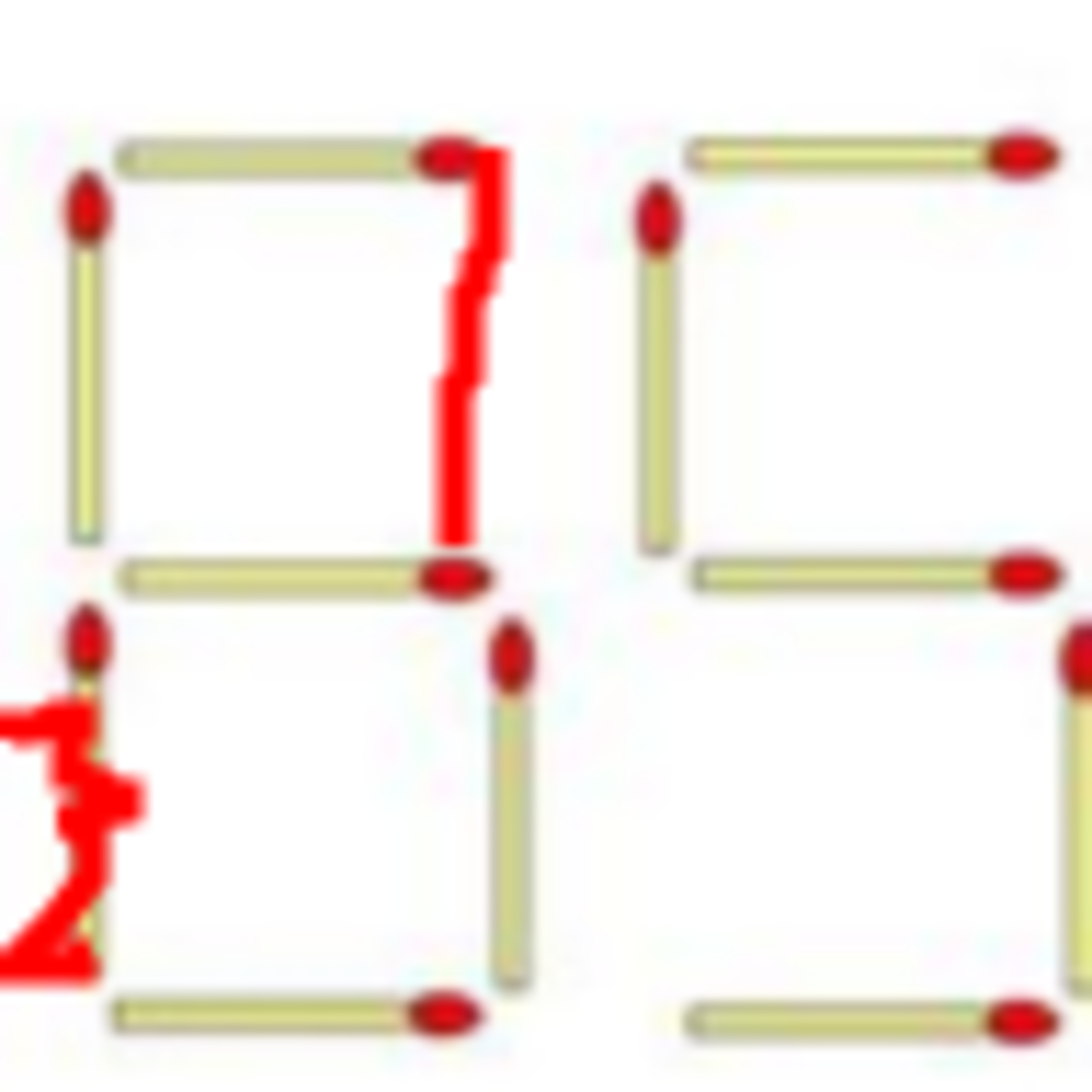
. this doe not have 4 as leading digit, so we move onto 3. but in the same case as 5, it cant lose 1 stick. we conclude that the 6 must lose a stick.
the only way(s) the 6 would make sense are
, but then the maximum possible product would be
8
5
×
1
3
=
1
1
0
5
. this doe not have 4 as leading digit, so we move onto 3. but in the same case as 5, it cant lose 1 stick. we conclude that the 6 must lose a stick.
the only way(s) the 6 would make sense are
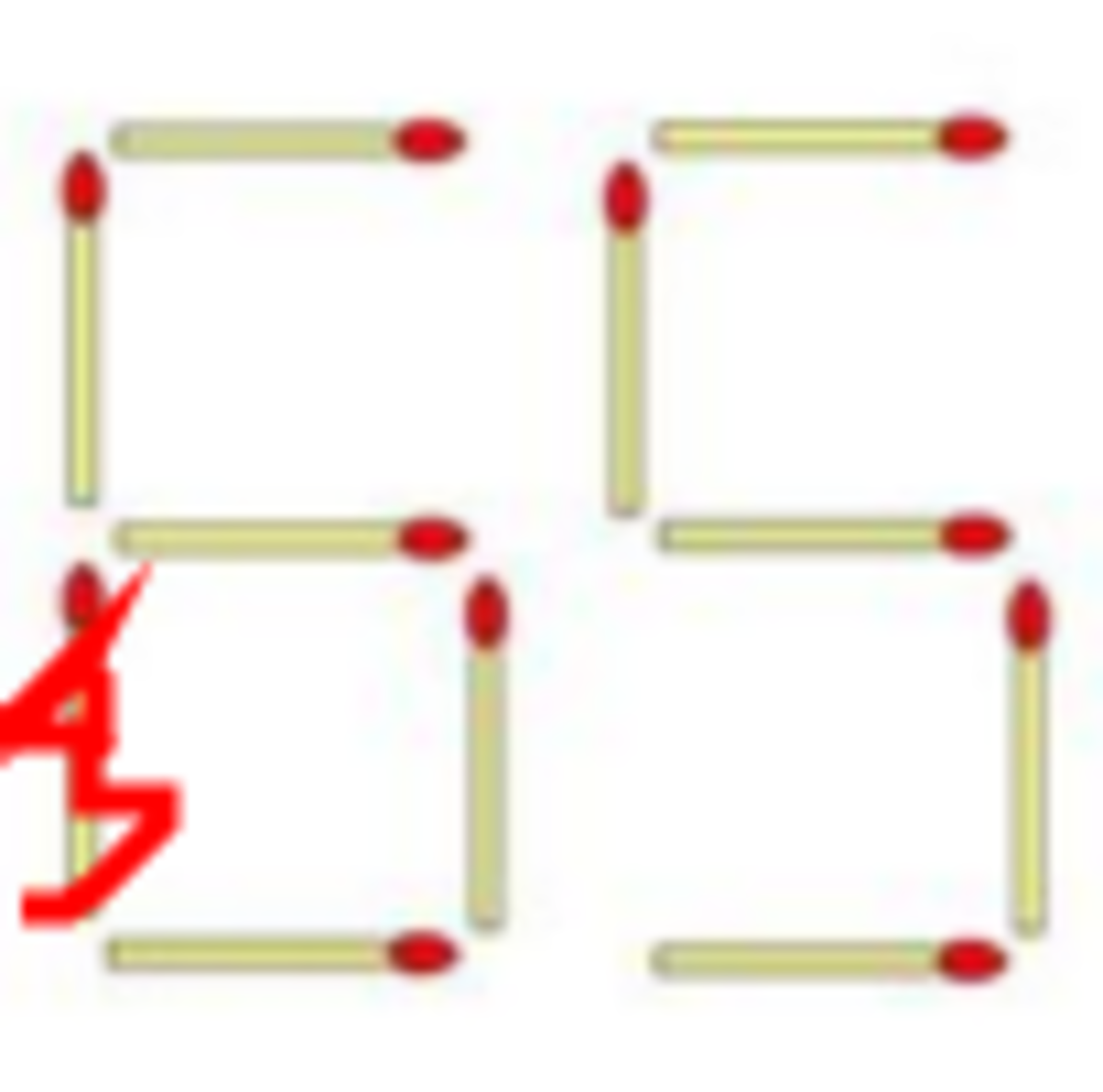 .
.
 at the latter case
9
5
∗
7
3
which will not have 4 as leading digit. we go to the scenario where 6 only loses a stick. the possible gains are to 5. but if five gained, the 2 possibles would be
5
9
×
7
3
=
4
3
0
7
,
5
6
×
7
3
=
4
0
8
8
. since non of this could be created by altering two sticks, we conclude 7 or 3 has to gain. you cannot add one stick to 7 and make sense of it. we give it to three who can only become9 and 6. we check and see the case with six doesnot make sense. we resort to nine and:
at the latter case
9
5
∗
7
3
which will not have 4 as leading digit. we go to the scenario where 6 only loses a stick. the possible gains are to 5. but if five gained, the 2 possibles would be
5
9
×
7
3
=
4
3
0
7
,
5
6
×
7
3
=
4
0
8
8
. since non of this could be created by altering two sticks, we conclude 7 or 3 has to gain. you cannot add one stick to 7 and make sense of it. we give it to three who can only become9 and 6. we check and see the case with six doesnot make sense. we resort to nine and: