Matchsticks Puzzle
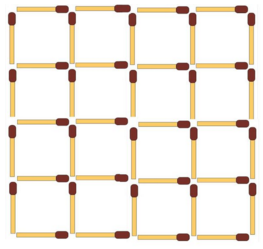
The diagram above shows 40 matchsticks arranged in a square grid.
What is the fewest number of matchsticks that need to be removed so that there are no squares (of any size) remaining?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
A slightly neater way is to reverse the order of consideration:
- For the 4X4 square, we must remove a matchstick from a border. This affects at most 1 1X1 square.
- For the remaining 15 1X1 squares. Removing any matchstick destroys at most 2 1X1 squares. Hence we will need at least 8 more matches.
- Thus we need at least 9 in total, and it remains to show that this can be done.
This avoids having to do the argument of "interior since we need each removed matchstick to destroy two squares", thereby cleaning it up slightly.
There's a 3 x 3 square in this picture (bottom right)
Log in to reply
I dont see itm...where is it mate?
Log in to reply
There are four 3x3 squares in the original problem - the fourth one (bottom right) is still in tact in picture above. See Pi's solution below for correct example of 9 matches removed demonstrating the solution
That's right; edited.
The solution is wrong. Picture shows a 3x3 square. Right ans will be 10. If anyone can solve by 9, please give a post.
Log in to reply
Log in to reply
Thanks!! You r right.
well i can see 4*4 square
my answer is 6...by removing 2nd from first row...1st ,3rd and 4th from 2nd row...1st and last from last row
That's right; the previous example was wrong. The answer is still 9, however; I've uploaded a correct example.
I can do it by removing 8 match sticks.
You can do it with 8, if you number the matchsticks that go vertically across, 1-5. Then remove matchsticks 2 and 4 from each row, making 2 rectangles on each row. 2 matchsticks per row, 4 rows. 8 matchsticks. Can you let me know if there is a problem with this! :)
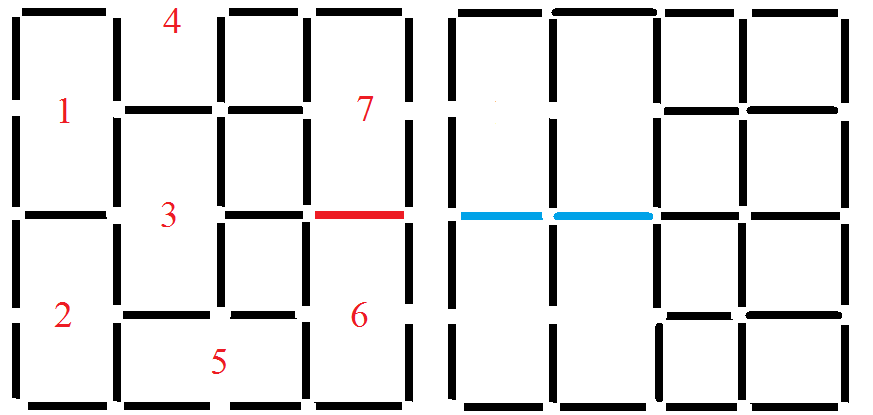 I found 9 on my own and it happens to be the same image as question master posted. (the above picture is created using MSpaint only)
I found 9 on my own and it happens to be the same image as question master posted. (the above picture is created using MSpaint only)
Anyway , for those who wondering how to get 9 , i decided to do a step by step reasoning. (every step has a meaning to it)
step 1 & 2 : we need to generate as much rectangle as possible , therefore step 1 & 2 makes it the fastest way.
STEP 3 : However in order to generate more rectangle we must avoid the scenario on the right side , as you can see the blue line becomes 2 x 2 square , if you attempted it yourself , i am sure you will be annoyed by one of the 2 blue lines.
Therefore step 3 is locked in the middle.
STEP 4 : having a twin 1 x 1 square on top and bottom after doing step 3 , its obvious that one of them has to become the sole single square. At this point you can choose to remove the outer boundary to eliminate 4x4 square from happening or just ignore it and continue building more RECTANGLE.
STEP 5 : you can only build a rectangle that way , if you do it other way which is removing the boundary just like step 4 , you will end up having a twin 1x1 square which better off to become rectangle in other way round.
STEP 6 & 7 : once you reach step 5 , you will notice that no matter what , the red line in between 6 & 7 CANNOT BE REMOVED. leaving you no choice but to go for step 6 & 7. (you can try and remove that red line after step 5 , i believe you will undo that action very soon)
step 8 and 9 should be obvious , try it yourself and end of explanation.
you can always refer back the picture above from question master for the remaining 2 stick
There's still 1x1 and 2x2 squares.
Log in to reply
i purposely left it out after i saw your picture above. there is no need for 2 complete set of answer in a solution page.
i am just posting the reasoning and step to reach it for those who are really trying by themself but still stuck at only removing 10 matchstick.
answer is not helping those who stuck at 10 match stick. so i did this.
( they can always refer back your picture to see the remaining 2 stick. )
simple solution, use logic guess...... ..
. . . . . . . . . . . . .
. .
LOL
Easiest Method!
Remove 4 vertical sticks in column 2
Remove 4 vertical sticks in column 4
Break the big square by removing 1 from the perimeter
By definition all remaining enclosed spaces are RECTANGLE not square
Remove all sticks frm 2nd and 4th row or 2nd and 4th column and remove 1 stick frm outside border
On dividing the above figure in half we get two rectangles of 2×4 (outer ones) on removing the 4 centre matchsticks for each rectangle(i.e.8 in total)will lead us to a figure having only recctangles(which are obviously not squares) but still we have one square left that is the bigger one 4×4 square and hence we have to remove one more match stick from the boundary of the 4×4 which would leads us to the desired answers.
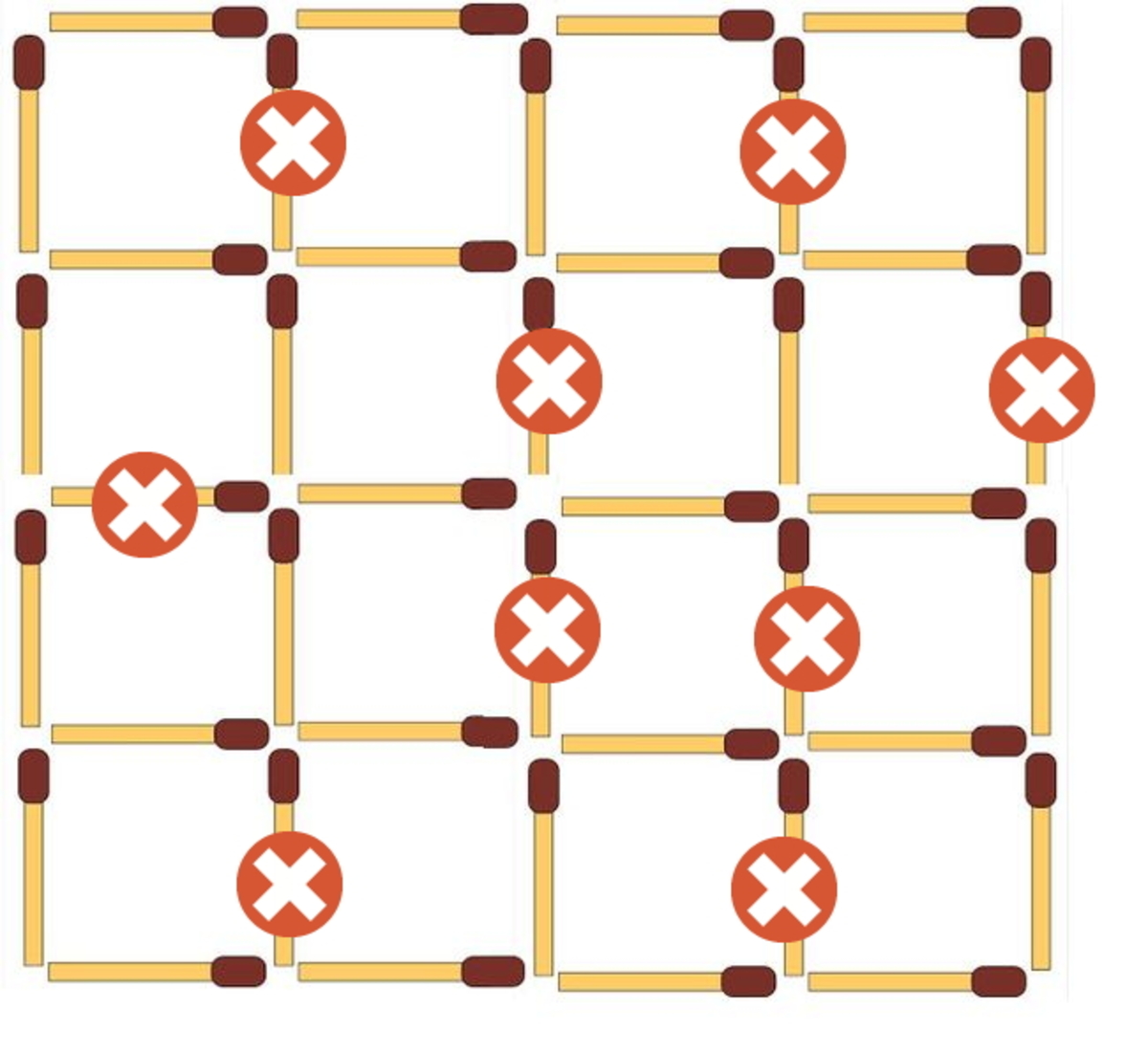
The outer 4 × 4 square requires one matchstick to be removed. This matchstick has to be from the outer border, which can only break one 1 × 1 square.
We have 15 1 × 1 squares remaining. Each time we remove a matchstick, we can only destroy two of them. Thus we need at least 8 more matchsticks removed, for a total of 9 . This is enough:
(Rewrote the solution to use Challenge Master's suggestions. As has been pointed out, the first version of this solution had a faulty example. Here's a fixed version.)