Math flag
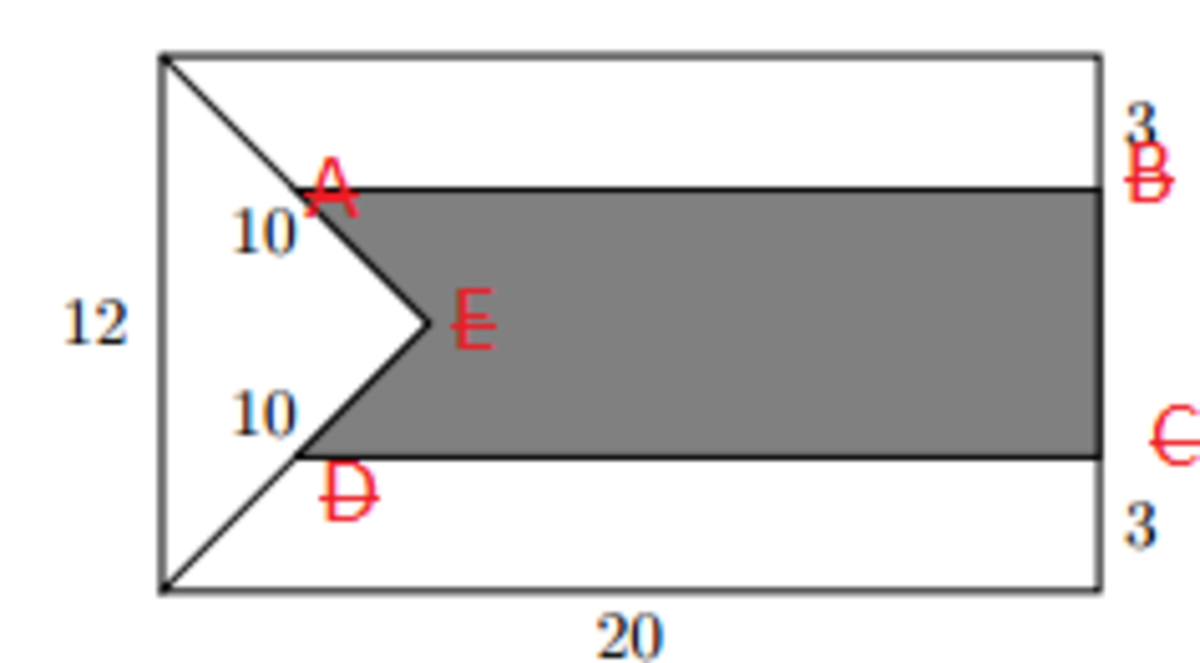
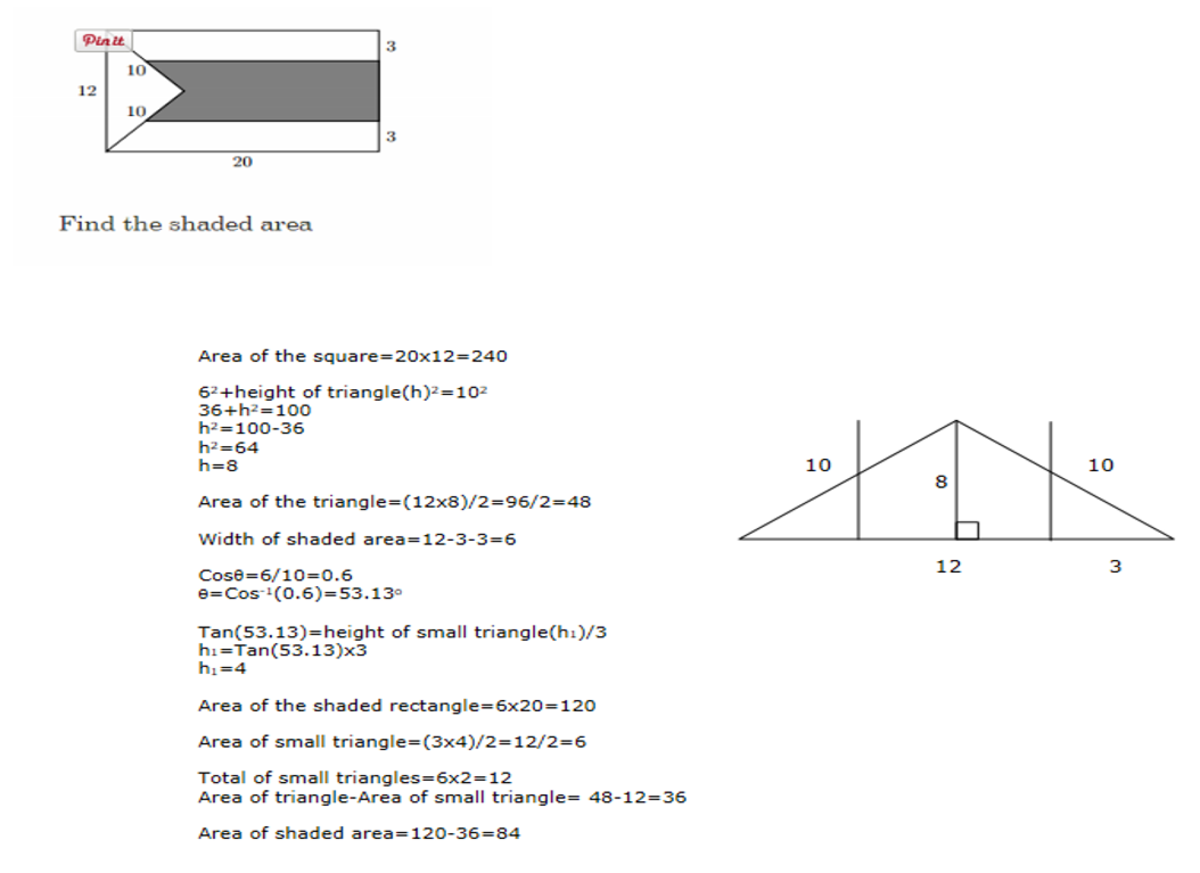
Find the area of the shaded region.
Details and Assumptions
We have an isosceles triangle with lengths 10, 10, 12.
The answer is 84.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
Does NA=AF? which is 5?
Yes it does
well i made a calculation mistake , so i got wrong ! i did it in diffrent manner whole fig has area 240sq units . so i found area for trianle NMF,MFN'(N'IS POINT present after N AND M . ) which was 48sq and then two smaller triangles which was 12sq and then the rectangles which was 96 . so 240 -96-60=240-156 = 84
I get it. Its just triangle similarities :)
We used Pythagorean Theorem
how did you get the altitude of the smaller triangle?
at paul: it's a 3-4-5 triangle. sqrt of 5^2 minus 3^2.
Denote the rectangle ABCD clockwise (from top-left). Extend the strip until it reaches AD. Now the area of this extended strip = 6 (width) × 20 = 120 (#1). Now we draw an altitude on the triangle and use Pythagoras's theorem to show that it's altitude is 8 (using the 2{3,4,5} Pythagorean triple) ⇒ area of triangle = 2 1 2 × 8 = 48 (#2). using (#1) we subtract this area from our extended strip: 120-48 = 72. However, we counted the two outer triangles '-1' times, so we slide them together to form a triangle that is half the scale factor of the large triangle, so it has a quarter of the area. Adding this on gives: Area of shaded strip = 72 + 4 4 8 = 72+12 = 8 4
close the shaded area as rectangle.
Area: Area of rectangle (ABCD) - Area of Triangle (ADE)
i.e (20 * 16) - (6 * 4)/2 = 96 -12 = 84
You can view the shaded area as two trapezoids.
We know the area of a trapezoid is 2 a + b h . To find base a and b, you need the height of the triangle left of the shaded region.
Split that triangle into two right triangles and you have a triangle with base 6 (12 / 2) and hypotenuse 10. Solve with the Pythagorean Theorem and you get the height of the triangle is 8.
Subtract that length from the total length of the rectangle (20) and you get the shorter base length is equal to 12. The other length extends to half the height of the triangle so it is length 16. The height of the trapezoid is 3 because it is 12 - 6 to get the height of the shaded area, divided by two to get the height of a trapezoid.
Solve for the trapezoid's area: 2 1 6 + 1 2 × 3 = 4 2
Since there are two triangles in the shaded area, the shaded area is 4 2 × 2
There it is: 84
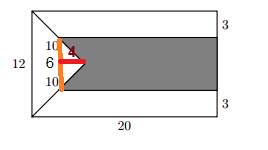
N M = 6 ⇒ M F 2 = 1 0 2 − 6 2 = 8
E A = M N − H B = 3 ∴ E A M N = E F M F = 2 ⇒ E F = 4
Shaded area is A B C D area − △ A F D area so
A B C D area is ( N H − M E ) ( 2 ( H G − H B ) ) = 1 6 ( 6 ) = 9 6
△ A F D area is 2 2 ( A E ) ( E F ) = 2 2 ( 3 ) ( 4 ) = 1 2
∴ shaded area is 9 6 − 1 2 = 8 4