Math in Daily Life: Walking to Work

Geometry Level 3

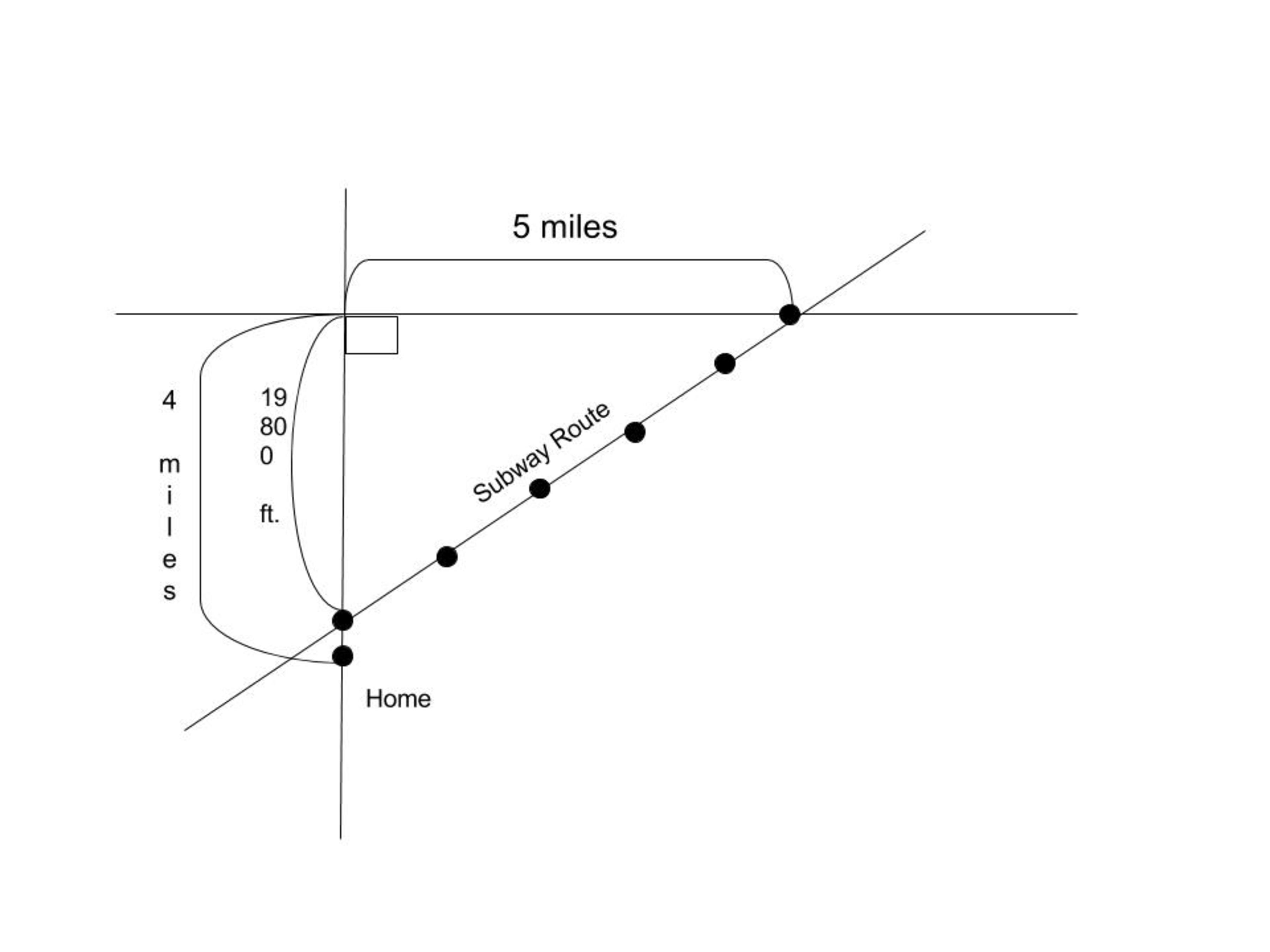
In order to get to work everyday, I drive my car on the highway. First, from home, I drive North for 4 miles. Then I turn right and drive for 5 miles. On average, I drive 30 mph the whole way. (Because of the daily rush hour.)

Later, a new subway was just finished, and provides an easier and quicker way for me to get to work. However, I have to walk to the newly constructed subway station. I bike on average 22 feet per second. The distance from the subway station to the intersection where I would usually turn right if I was driving my car is 19800 feet. The subway train runs 30 mph on average, and makes 1 minute stops at each station. There are 4 stations in-between the station I get on the subway train and the station I get off of to go to work.

Is taking the subway to work faster than driving my car to work? If so, by how many seconds?

Assumptions:

Do not include the time used in-between to start the car, walk into the station and train, walk to work, turn the car, back out of the driveway, etc.
Nothing special is going on.
Average speed is consistent throughout the ride to work.

There is not enough information to determine if the subway or car is faster. The car is faster by 60 seconds The car is faster by 30 seconds The subway is faster by 30 seconds. The subway is faster by 90 seconds The subway is faster by 15 seconds The subway is faster by 60 seconds

1 solution

William Pan
Dec 23, 2015

By car, you will take 18 minutes to get to work, since you go 30 mph for 9 miles.

The subway route from the station you get on the subway to the station your work office is located at is 6.25 miles long, or 33,000 feet, by Pythagorean Theorem.

${ \qquad \quad \qquad \quad \quad a }^{ 2 }\quad +\quad { b }^{ 2 }\quad ={ \quad c }^{ 2 }\\ \quad \quad { 19800 }^{ 2 }\quad +{ \quad (4\times 5280) }^{ 2 }={ \quad c }^{ 2 }\\ \quad \quad \quad \quad \quad \sqrt { { 19800 }^{ 2 }+{ 26400 }^{ 2 } } =\quad c\\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \therefore \quad c\quad =\quad 33000$

From your house to the subway station, you would bike for 1 minute (60 seconds), as you are biking for 1320 feet (4 miles minus 19800 feet) at a speed of 22 feet per second, and 1320 divided by 22 is 60.

The subway train runs at 30 mph and the track from the station where you board the train to the station your work office is located is 6.25 miles. Therefore, the subway train will take 12.5 minutes nonstop to get to your destination. But, there are 4 stations in-between, meaning there are four one-minute stops. You must add four minutes to the route, which adds up to 16.5 minutes. You must also include the time you bike to the subway station, which is one minute. So, taking the subway will take 17.5 minutes.

Since 17.5 < 18, taking the subway will take less time. 18 minutes - 17.5 minutes = 30 seconds, so taking the subway will be 30 seconds faster than driving a car to work, as long as there are no interruptions or obstacles.

Math in Daily Life: Walking to Work

1 solution

0 pending reports