This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Chew-Seong Cheong Sir nice solution, i was thinking one with vieta formula but nice solution!!
You can't just ignore the (x^2+x+1)!
Log in to reply
There are no real solutions to x 2 + x + 1 = 0
Just applied componendo-dividendo
4 x 2 + 1 5 x + 1 7 + ( x 2 + 4 x + 1 2 ) 4 x 2 + 1 5 x + 1 7 − ( x 2 + 4 x + 1 2 ) = 5 x 2 + 1 6 x + 1 8 + ( 2 x 2 + 5 x + 1 8 ) 5 x 2 + 1 6 x + 1 8 − ( 2 x 2 + 5 x + 1 8 ) ⇒ 5 x 2 + 1 9 x + 2 9 3 x 2 + 1 1 x + 5 = 7 x 2 + 2 1 x + 3 1 3 x 2 + 1 1 x + 5
Now the factors are easily visible.
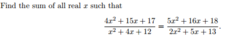
x 2 + 4 x + 1 2 4 x 2 + 1 5 x + 1 7 = 2 x 2 + 5 x + 1 3 5 x 2 + 1 6 x + 1 8
⇒ x 2 + 4 x + 1 2 4 x 2 + 1 5 x + 1 7 = x 2 + 4 x + 1 2 + x 2 + x + 1 4 x 2 + 1 5 x + 1 7 + x 2 + x + 1
( 4 x 2 + 1 5 x + 1 7 ) ( x 2 + 4 x + 1 2 ) + ( 4 x 2 + 1 5 x + 1 7 ) ( x 2 + x + 1 ) = ( 4 x 2 + 1 5 x + 1 7 ) ( x 2 + 4 x + 1 2 ) + ( x 2 + 4 x + 1 2 ) ( x 2 + x + 1 )
( 4 x 2 + 1 5 x + 1 7 ) ( x 2 + x + 1 ) = ( x 2 + 4 x + 1 2 ) ( x 2 + x + 1 )
4 x 2 + 1 5 x + 1 7 = x 2 + 4 x + 1 2 ⇒ 3 x 2 + 1 1 x + 5 = 0
⇒ x = 6 − 1 1 ± 1 2 1 − 6 0 = 6 − 1 1 ± 6 1
The required solution = 6 − 1 1 + 6 1 + 6 − 1 1 − 6 1 = 3 − 1 1 ≈ − 3 . 6 7