Math Problem from a magazine
Positive real numbers a and b are such that a + b = 4 5 . Find the minimum value of
P = a 4 + 4 b 1
Bonus: Show as many ways to solve this problem as possible.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Method 1: Using Derivatives
a + b = 4 5 → b = 4 5 − a
P = a 4 + 4 ( 4 5 − a ) 1 = a 4 + 5 − 4 a 1
P ′ = − a 2 4 + ( 5 − 4 a ) 2 4 = 0 (and P ′ ′ > 0 for 0 < a ≤ 4 5 ) → a = 1 → P = 5
Method 2: Using Derivatives
a + b = 4 5 → a = 4 5 − b
P = 4 5 − b 4 + 4 b 1 = 5 − 4 b 1 6 + 4 b 1
P ′ = ( 5 − 4 b ) 2 6 4 − 4 b 2 1 = 0 (and P ′ ′ > 0 for 0 < b ≤ 4 5 ) → b = 4 1 → P = 5
Method 3: Using Graphing Technology
Graph P = a 4 + 5 − 4 a 1 from Method 1
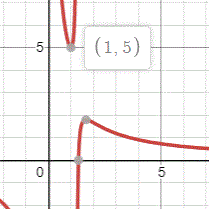
Method 4: Using Graphing Technology
Graph P = 5 − 4 b 1 6 + 4 b 1 from Method 2
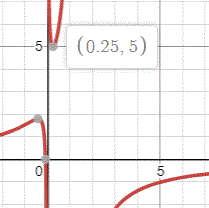
P = a 4 + 4 b 1 = 5 4 ( a + b ) ( a 4 + 4 b 1 ) = 5 4 ( 4 + 4 1 + a 4 b + 4 b a ) ≥ 5 4 ( 4 + 4 1 + 2 a 4 b ⋅ 4 b a ) ( B y A M − G M I n e q u a l i t y ) = 5 4 × 4 2 5 = 5
Notice that this method only works with 2 terms. To solve cases with over 3 terms, we need to consult Cauchy-Schwarz Inequality, or Titu's lemma.
-
Solution 1: 4/a + 1/4b = 4^2/4a + 1^2/4b >= (4+1)^2 / 4(a+b) = 5
-
Solution 2: 4/a + 4a >= 8, 1/4b + 4b >= 2 => 4/a + 1/4b + 4(a+b) >= 10 => P >= 10 - 4*5/4 = 5
-
Min P = 5 when a = 1, b = 1/4
Method 1: By Titu's lemma
a 1 2 + a 1 2 + a 1 2 + a 1 2 + 4 b 1 2 ≥ 4 ( a + b ) ( 1 + 1 + 1 + 1 + 1 ) 2 = 4 × 4 5 5 2 = 5 Equality occurs when a = 1 , b = 4 1
Method 2: By AM-HM inequality
a 1 + a 1 + a 1 + a 1 + 4 b 1 5 ⟹ a 4 + 4 b 1 ≤ 5 a + a + a + a + 4 b ≥ 4 ( a + b ) 5 2 = 5 Equality occurs when a = 1 , b = 4 1
Method 3: By Hölder's inequality
( a 1 + a 1 + a 1 + a 1 + 4 b 1 ) ( a + a + a + a + 4 b ) ( a 4 + 4 b 1 ) ( 4 ) ( a + b ) ⟹ a 4 + 4 b 1 ≥ ( 1 + 1 + 1 + 1 + 1 ) 2 ≥ 2 5 ≥ 5 Equality occurs when a = 1 , b = 4 1