Mathathon Sample Question
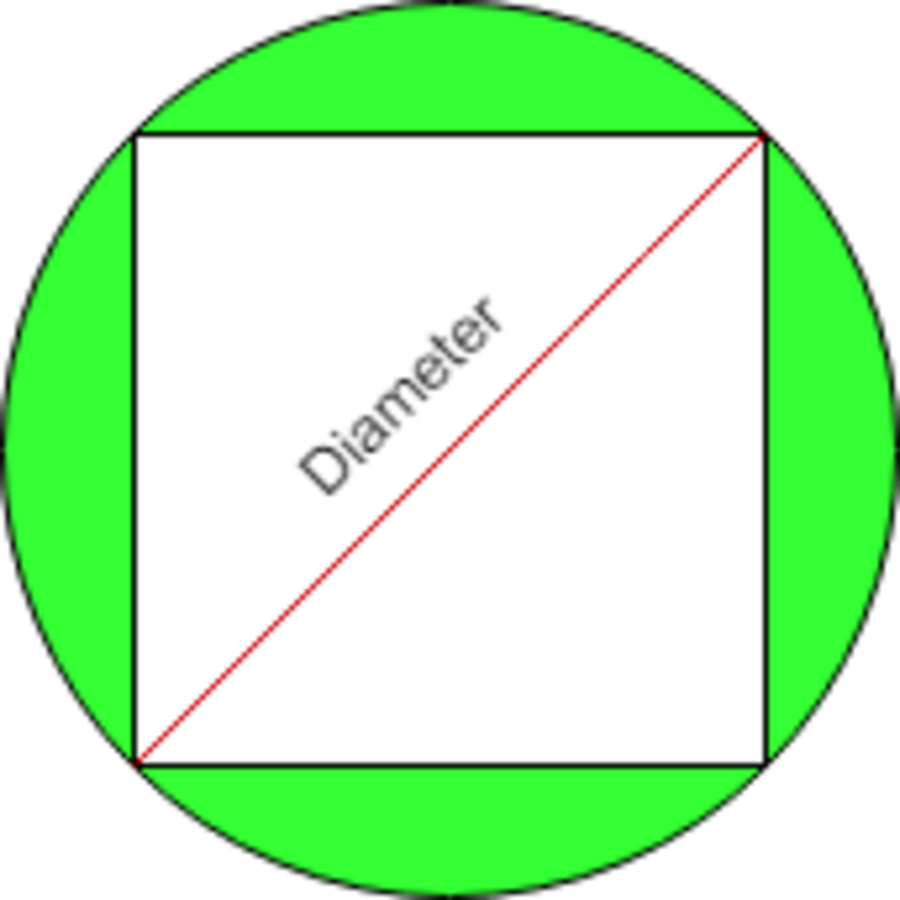
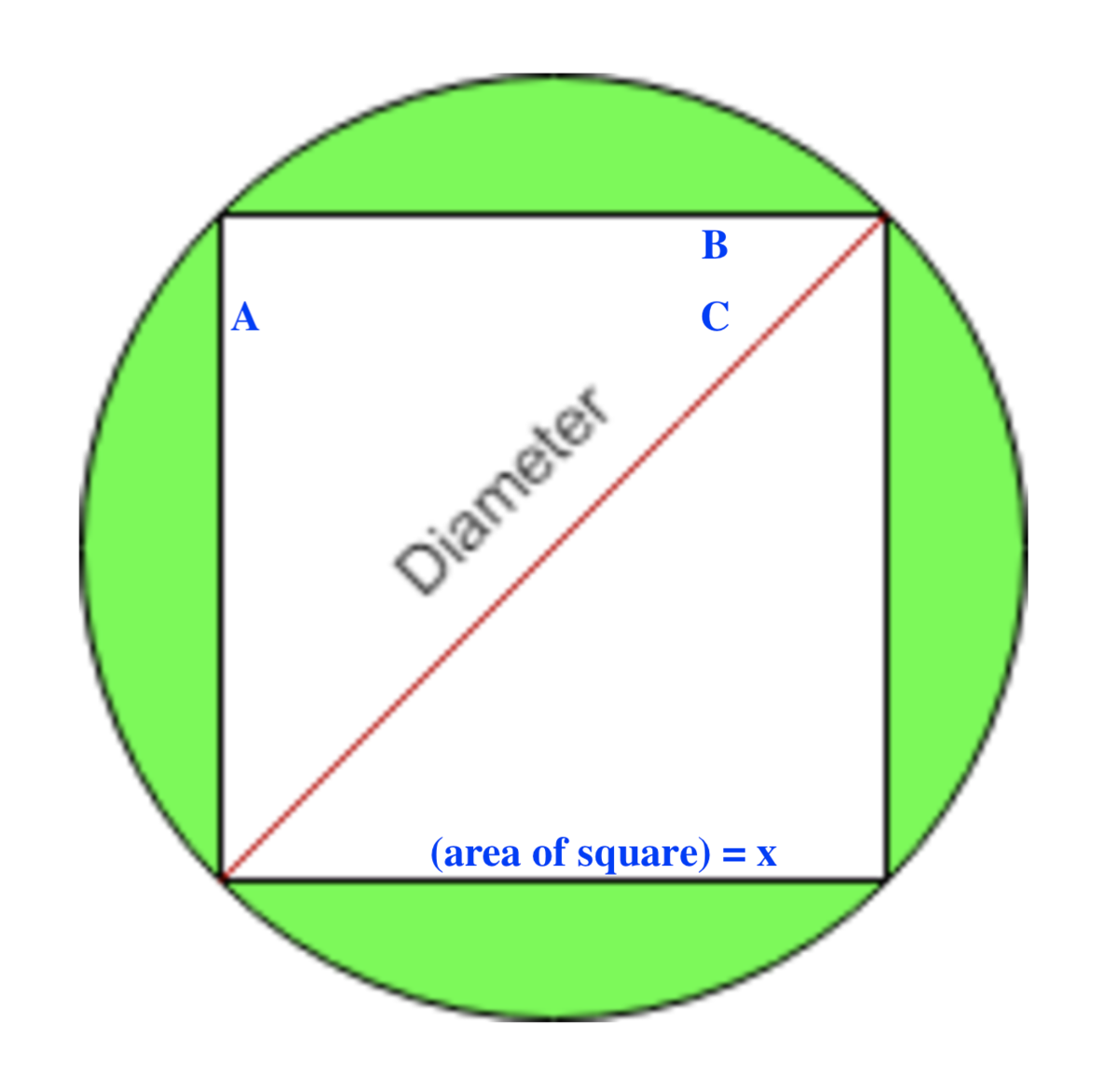
The cyclic quadrilateral in the circle shown above is a square. The diameter of the circle is 5 . Find the area of the square.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Area Of square = 2 d i a g o n a l 1 × d i a g o n a l 2 (Square is a rhombus)
diagonal1 = diagonal2 = Diameter of circle = 5
Area = 2 5 × 5
A r e a = 1 2 . 5
Nice! Unique solution @Aryan Sanghi ! I hadn't even thought of that formula!
If you don't know about Mathathon 2020 yet, please register here and read the guidelines before posting a solution. Thank you everyone.
The avatar looks really cool. Are you actually Percy Jackson?🙃
Log in to reply
Almost actually :) (up to you to figure out the meaning of that) @Lin Le
Diagonal = 5
Pythagoras Theorem → x 2 + x 2 = 5 2 ( x is side length of square)
x 2 = 1 2 . 5
Sh*t my puny mind!
The square can be divided into 2 45-45-90 degree triangles.
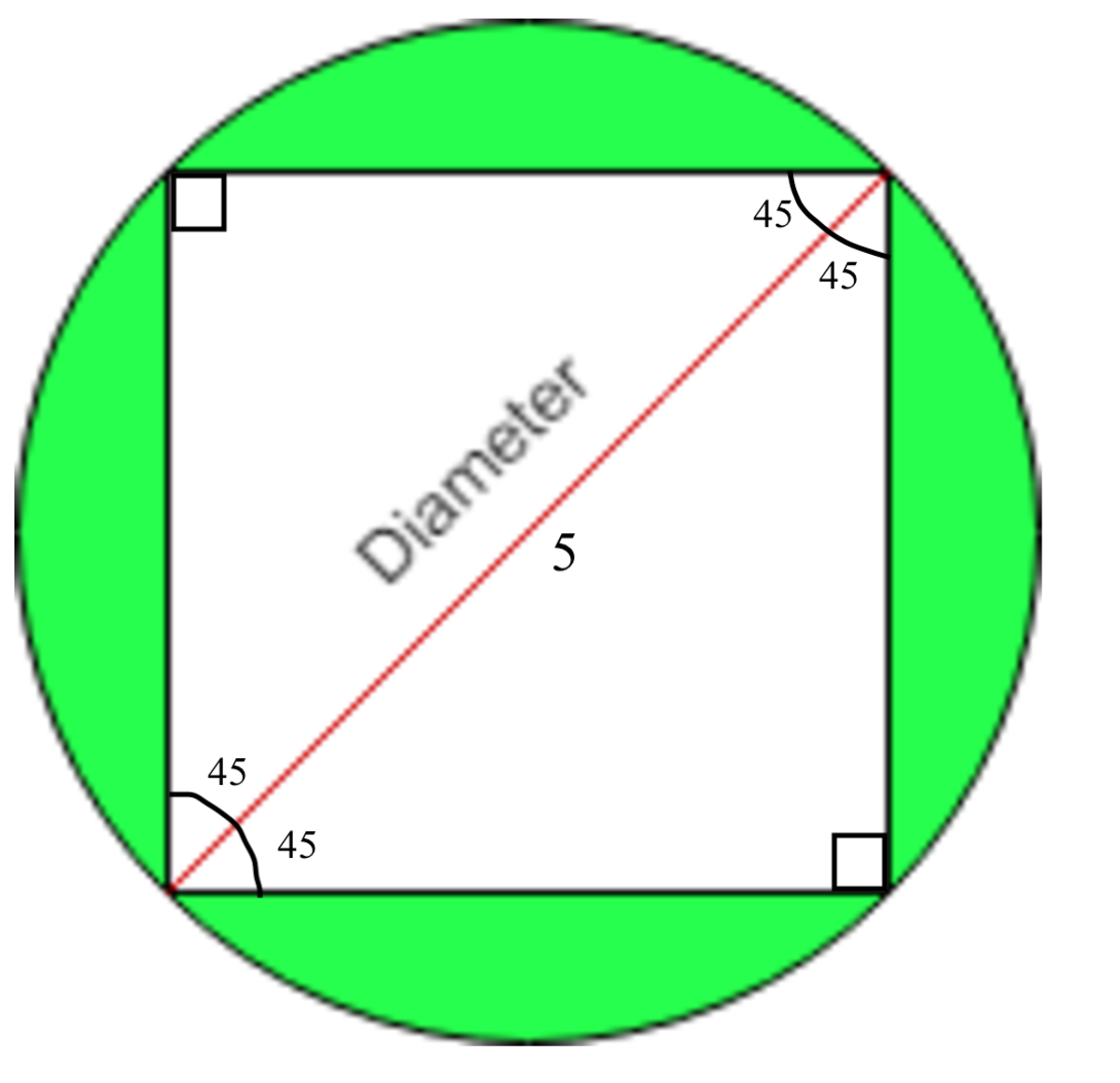
The hypotenuse of a 45-45-90 triangle is 2 times more than the sides.
So the side length is 2 5 .
The area of a square is s 2
2 2 5 2 = 2 2 5 = 1 2 . 5
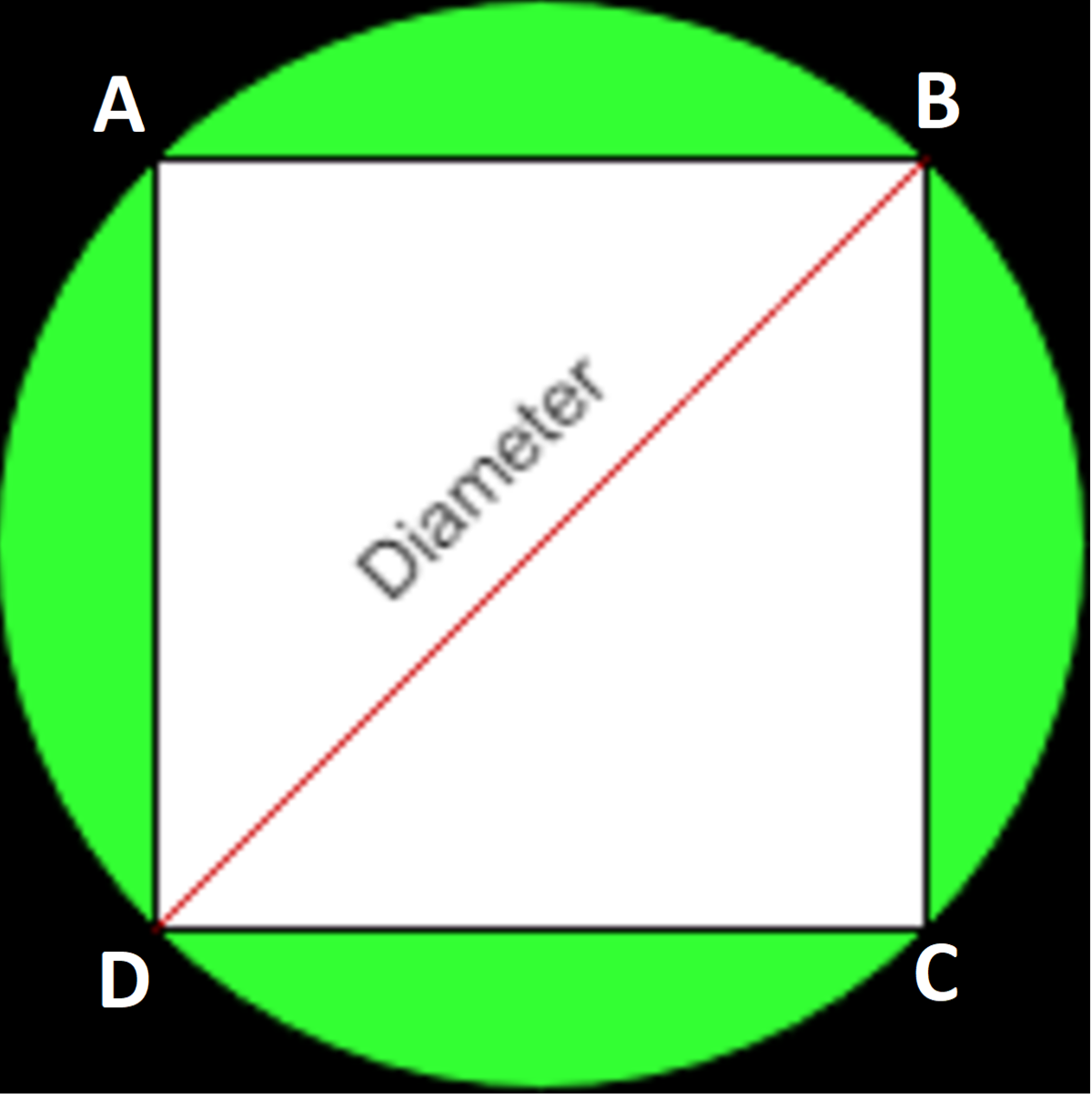 As
A
B
C
D
is a square
∴
∠
B
C
D
=
9
0
°
As
A
B
C
D
is a square
∴
∠
B
C
D
=
9
0
°
⇒ △ B C D is a right angled triangle. Applying Pythagorus theorem B C 2 + C D 2 = B D 2 As B C = C D because A B C D is a square ∴ B C 2 + B C 2 = B D 2 2 B C 2 = B D 2 B C 2 = 2 1 B D 2 As B D = d i a m e t e r = 5 c m ∴ B C 2 = 2 1 × ( 5 c m ) 2 = 2 1 × 2 5 c m 2 = 1 2 . 5 c m 2 Area of A B C D = B C 2 = 1 2 . 5 c m 2
Pythagoras' Theorem
a 2 + b 2 = c 2
As a = b
2 a 2 = c 2
2 a 2 = 5 2
2 2 a 2 = 2 5 2
a 2 = 1 2 . 5
As the area of the square is = a 2 (where a is the side of the square)
The area of the square is = 12.5
@Percy Jackson , I now only saw your post
Approx. before 10 mins
- x^2+x^2=5^2 (pythagorean theorem)
- x=side length of square
- side length = 3.53
- area=3.53^2
- 12.5
Awesome! Use \ ( \ ) to make your numbers look bigger, and more pleasing :)
There are 3 main ways:
1.
Since the quadrilateral is a square, it’s side length is:
2
s
2
=
2
5
⇒
s
2
=
1
2
.
5
Where
s
is it’s side length. Note that we
don’t even need to find
s
.
2.
.
Split the square into two right angled isosceles triangles.
The size of two triangles is:
5
×
2
5
×
2
=
1
2
.
5
.
3.
The size of the square is half of a square with side length equal to its diagonal, so
S
□
=
2
5
2
=
1
2
.
5
.
Learn more in RadMaths !
-
A 2 + B 2 = C 2
-
A 2 = B 2 = x
-
C 2 = 5 2 = 2 5
-
2 x = 2 5
Q . E . D . : x = 2 5 / 2 = 1 2 . 5
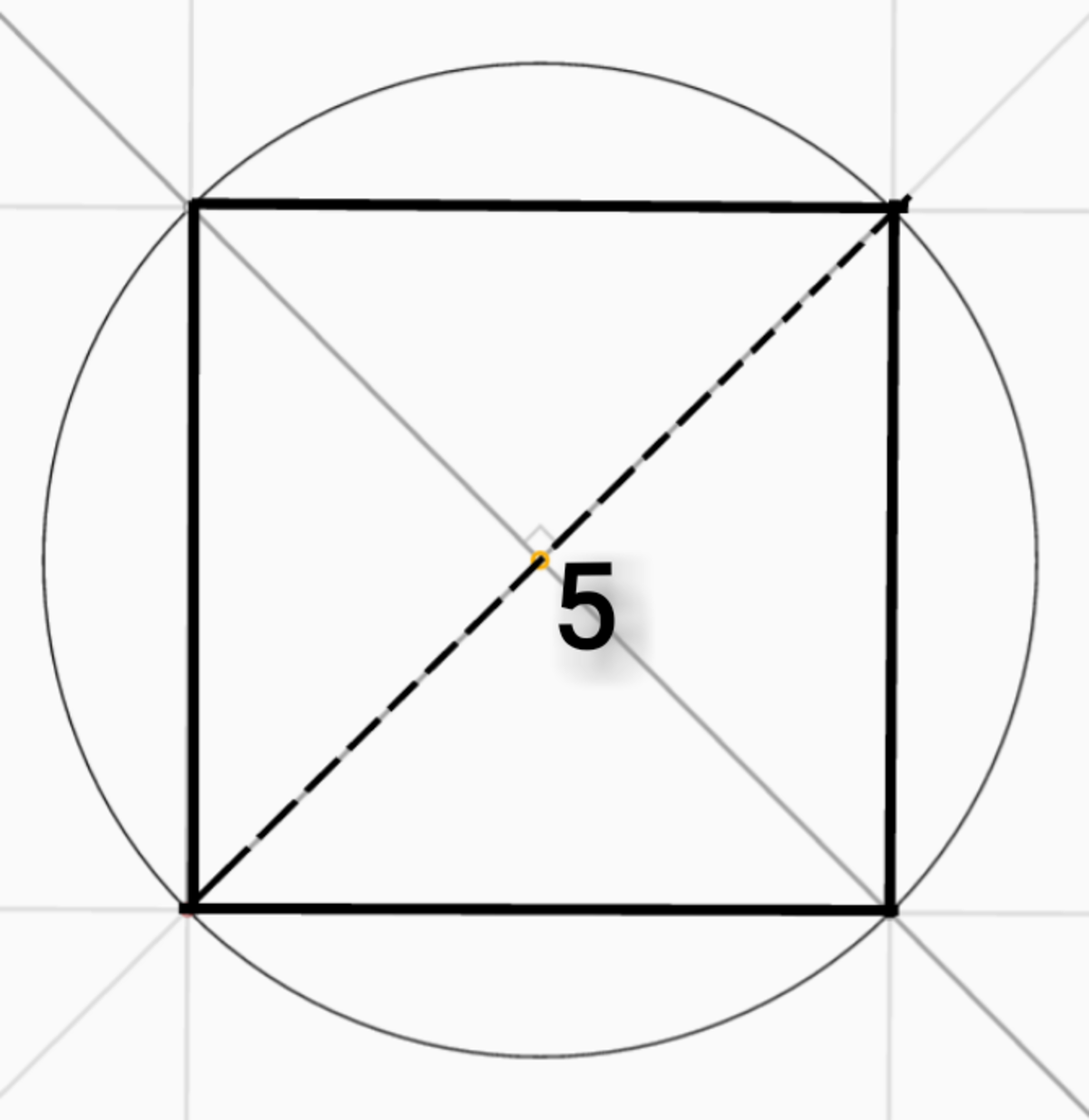
Although there are many ways to solve this problem, the easiest and quickest way is to rearrange the square into half of a new square, like this:
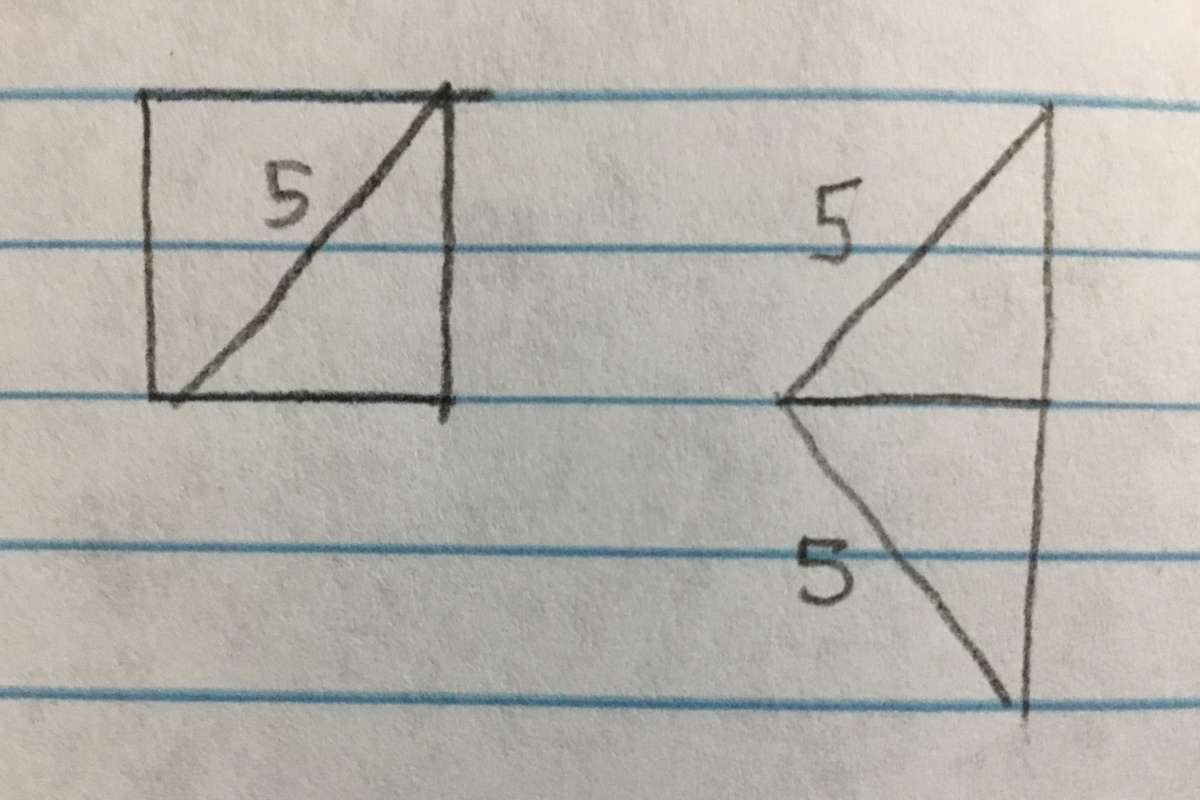
Since we bisected the square, the 9 0 degree angle was split into two 4 5 degree angles. Thus, when we rearrange the parts, combining the two 4 5 degree angles will give us back a 9 0 degree angle, which proves that the resulting figure is half of a new square.
This makes it so much easier! The new square's area is 5 × 5 = 2 5 units squared. Half of the area of this square is 2 1 × 2 5 = 1 2 . 5 units squared, our answer.
@Ved Pradhan , I think you should include the proof as to why the 2 triangles form half a square (45 degrees + 45 degrees)
Log in to reply
Thanks, @Percy Jackson ! I have added that to my solution.
Log in to reply
Great solution Ved, its great now!
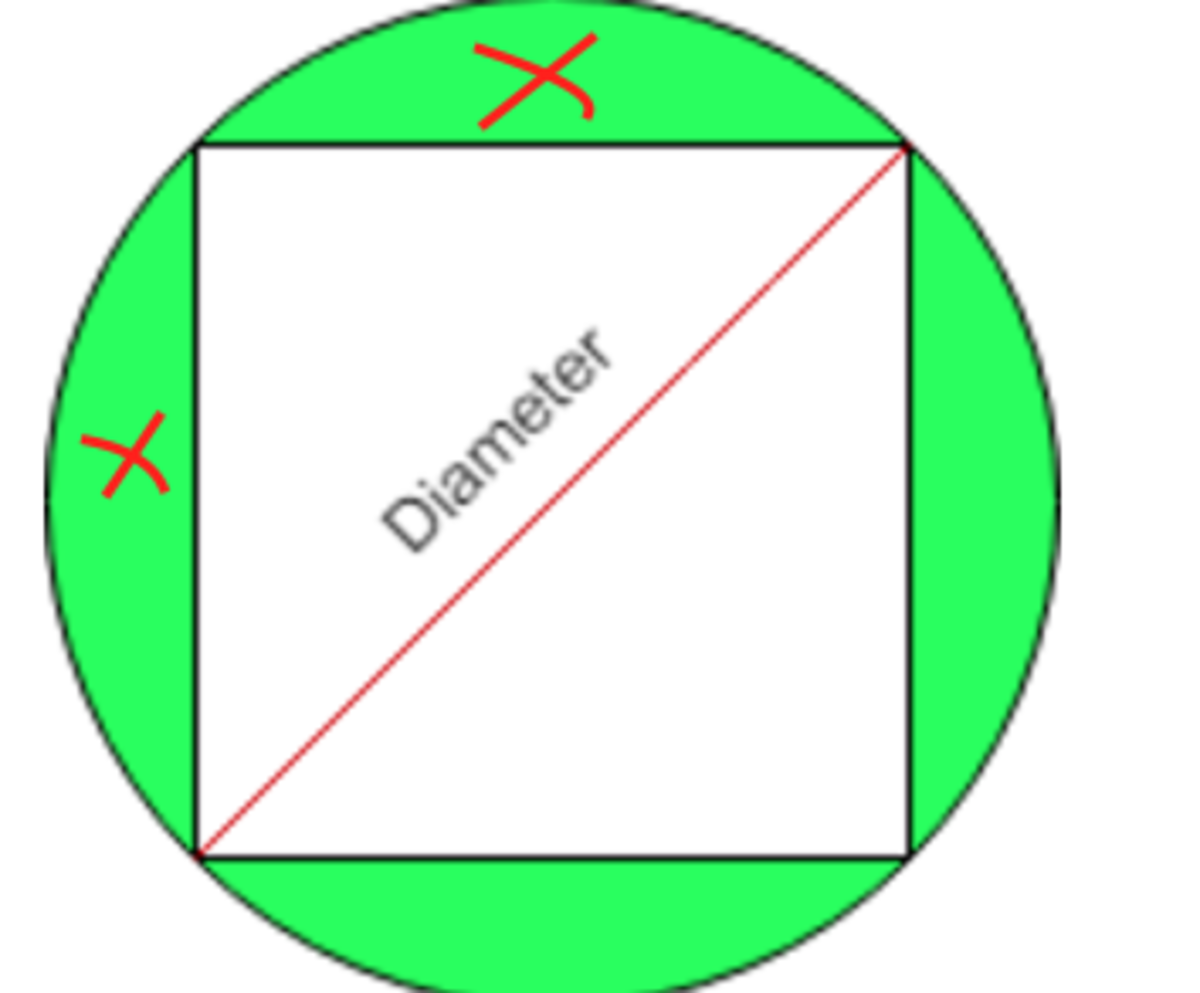 x
2
= area
Pythagorean theorem:
x
2
= area
Pythagorean theorem:
x 2 + x 2 = 5 2
2 x 2 = 2 5
x 2 = 1 2 . 5
a r e a = 1 2 . 5
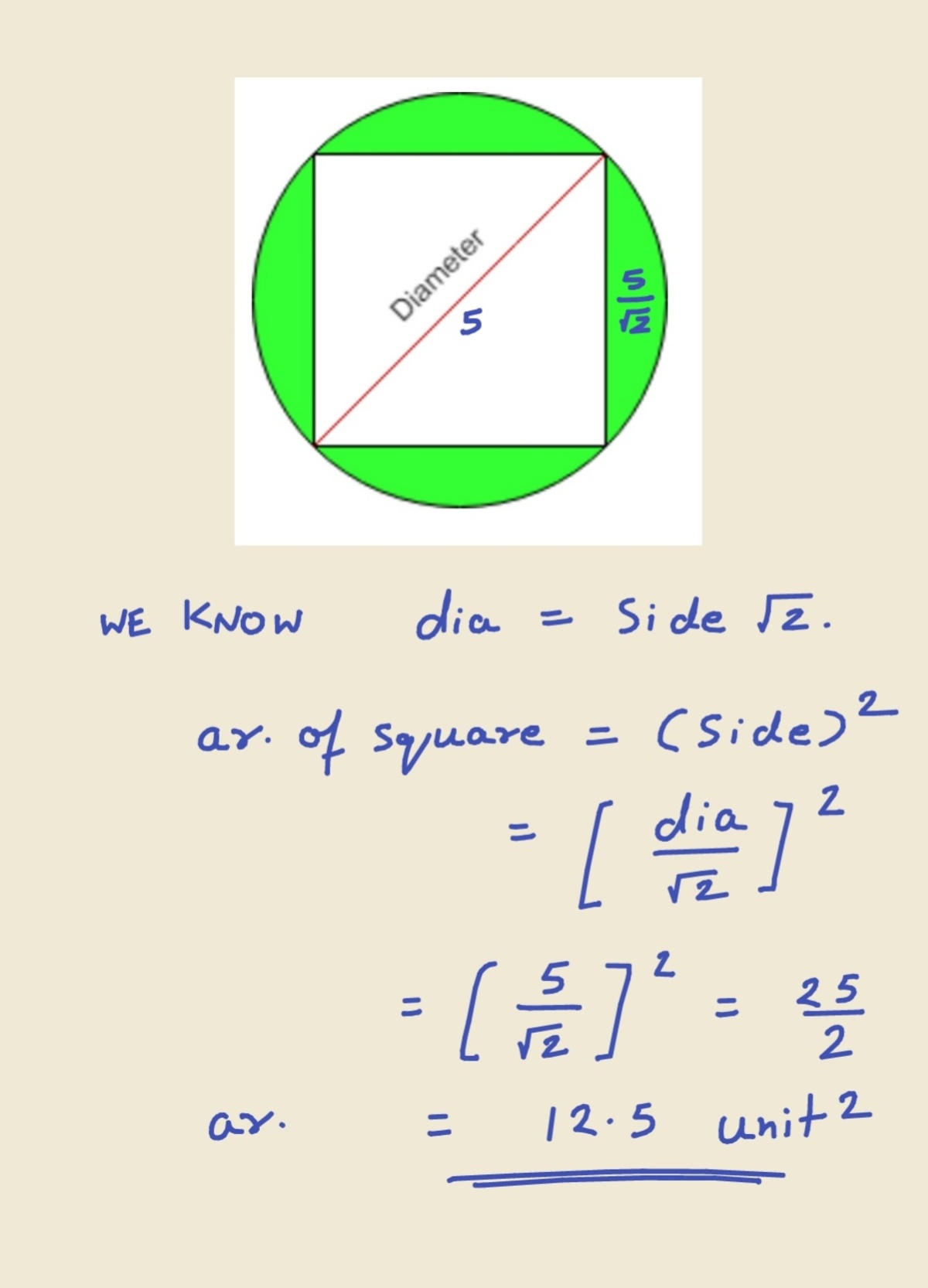
Since ,angle ABC = 90 degree.
Now, s i d e 2 + s i d e 2 = A C 2
s i d e 2 = 1 2 . 5
a r e a = 1 2 . 5