Mathematical Cavalcade revisited
Brilly the ant stands at point A , in a distance of 25 cm from a cylindrical glass beaker. At point C inside the far side of the beaker and 6 cm below its rim, there is a drop of honey. The circumference of the beaker is 16 cm , and it stands 9 cm high. Brilly the (lazy) ant wants to take the shortest route to reach the honey. If that distance is x cm , then,
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I agree x<42. However, it seems like the shortest distance is 40.8 (sketch below). Am I misinterpreting the geometry? Thank you for putting up the problem and solution!
How do you know that the best point to reach the beaker is between B and E ? That is, can you prove that the ant reaching at any point outside B and E will result in it travelling a longer distance ?
Log in to reply
Due to symmetry, in the solution I considered only the semi-space defined by the plane through AO, perpendicular to ground level. There, if the ant wants to reach any point outside B and E, he must fist reach point E, but then the shortest path form E to C is obtained when moving up the curved surface of the beaker and follow a path similar to DC' in figure 2 (put E in the place of D). This means that if he goes any further along the beaker's circular base, past E, he will result in a longer path.
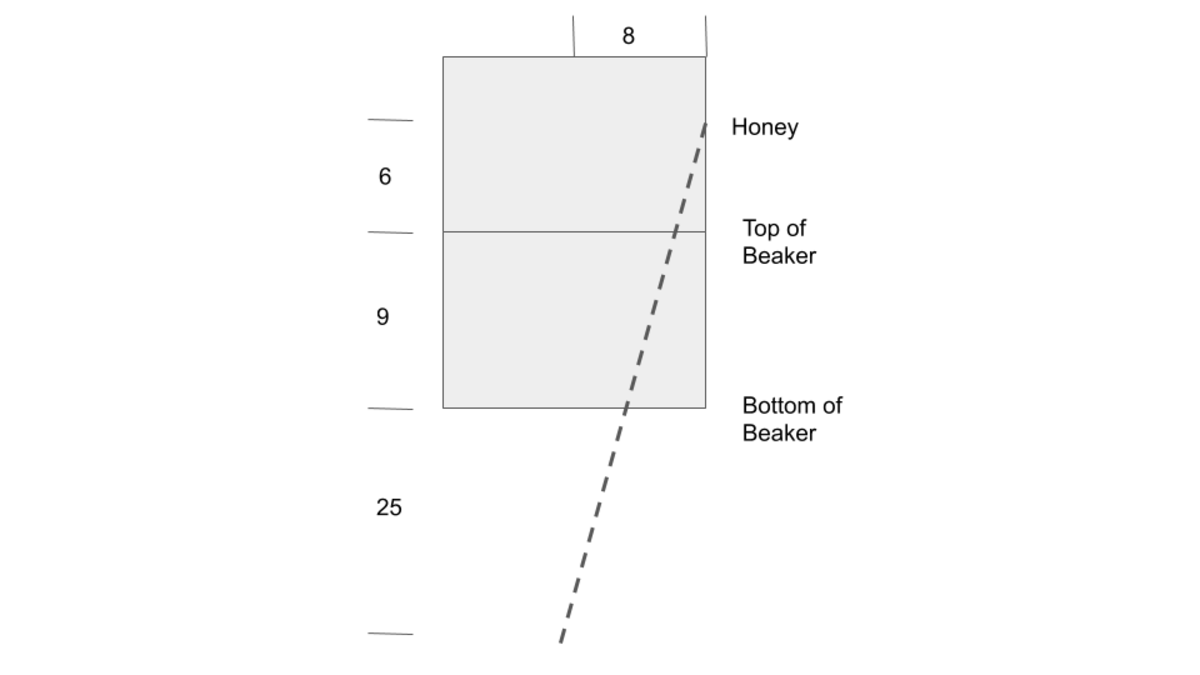
I used the theory that the shortest distance between two points is a line: d = 4 0 2 + 8 2 = 4 0 . 8 < 4 1 . 7 7 . What am I missing here?
Cool problem!
You worked under the assumption that you can open flat the curved surface of the beaker together with the plane containing point
A
and the first part of Brilli's path. When you do that, there is a small part of the path that gets lost. I made a figure to depict it, as segment
Z
W
.

Oh, gosh, you are right! Thank you! (Also, really nice depiction of my dumbery!)
The shortest path length must be less than 2 5 + 2 1 6 + ( 9 − 6 ) or 3 6 cm. Hence it is obviously less than 4 2 cm.
The drop of honey Brilli the ant wants to reach is inside the beaker. So it needs to climb up to the rim of the beaker and then descent from the inner side of the curved surface to get to point C.
No, ant has to first climb up the beaker because it's inside.
Ok My answer it's pretty different from all of this, first I flattened out the beaker then I noticed that the point c was in the middle so I use the hypotenuse=√9²+8²=12 then to that I added the 25cm that is between point A to point B and the result was 12+25=37 so the answer will be x<42 But please help because I think I'm wrong :'(
@rovati 10 - I think you missed the fact that the drop of honey is inside the baker, so Brilli the ant must climb up to the rim of the beaker and then descent from the inner side of the curved surface to get to point C. These extra 6 cm give to your approach a total distance travelled of 43 cm which is not the best we can get.
I found this problem in Brian Bolt’s well-known book, entitled “Mathematical Cavalcade”. The book is a collection of interesting and very amusing recreational mathematical problems. This is the only puzzle in the book where I spotted a flaw. Hints and solutions are given in a commentary at the back of the book. There, the answer stated is 4 2 . As we shall see, a better solution exists. figure 1
figure 1
Let O be the center of the circular beaker’s base (figure 1). The radius of the circle is R = π 8 . Brilli the ant can reach the base of the beaker, say at point D , between B and E ( A E is tangent to the circle).
Denote the length of B D ⌢ by s and let ∠ A O D = θ . Then, θ = R s and by cosine rule A D 2 = A O 2 + R 2 − 2 A O ⋅ R ⋅ cos θ ⇒ A D = ( 2 5 + π 8 ) 2 + ( π 8 ) 2 − 2 ( 2 5 + π 8 ) ⋅ π 8 ⋅ cos ( 8 π s ) s ∈ I : = [ 0 , π 8 ⋅ cos − 1 2 5 π + 8 8 ] ≈ [ 0 , 3 . 7 6 ] ( 1 )
If we flatten out half of the curved surface of the beaker we come with a rectangle B F G H , with point C on F G (figure 2). Reflect point C on G H to point C ′ .
Then, D P + P C = D P + P C ′ ≥ D C ′ = ( 8 − s ) 2 + 1 5 2 ( 2 )
Combining ( 1 ) and ( 2 ) , we have the minimum distance from A to C as a function of s :
f ( s ) = ( 2 5 + π 8 ) 2 + ( π 8 ) 2 − 2 ⋅ ( 2 5 + π 8 ) ⋅ π 8 ⋅ cos ( 8 s ⋅ π ) + ( 8 − s ) 2 + 2 2 5 , s ∈ I The derivative of f is
In other words, for s ∈ I 1 , s = 0 ,
f ( s ) < f ( 0 ) = 4 2 In fact, at s 1 ≈ 1 . 0 1 f gives its minimum, which is f ( s 1 ) ≈ 4 1 . 7 7 (figure 3).
Hence, the correct answer is x < 4 2 .