Mathematical Enigma- V
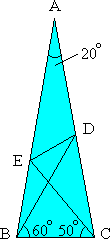
Let ABC be an isosceles triangle ( with . Point is on side such that . Point is on side such that . Find the measure of .
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Observe that angle(BEC)=50°, angle(BDC)=40° and BE=BC. Take the point "F" on DC, such that angle(CBF)=20°. Observe that the triangle BFC is isosceles with BC=BF. Then BF=BE with angle(EBF)=60°, and the triangle BEF is equilateral. As the angle(BDC)=40°, then the triangle BFD is isosceles, so BF=FD, and since EF=BF=BE then DF=EF. The angle(EFD)=40° since angle(BFC)=80°, and the triangle EFD is isosceles; so angle(EDF)=70° and we will angle(EDB)= 30°.