Mathematical Enigma - XIII

By extended AM-GM inequality,
$a^bb^a+a^ab^b$
$=\sqrt[a+b]{a^bb^a}+\sqrt[a+b]{a^ab^b}$
$\le \dfrac{ab+ba}{a+b} + \dfrac{aa+bb}{a+b}$
$=a+b$
$=1$

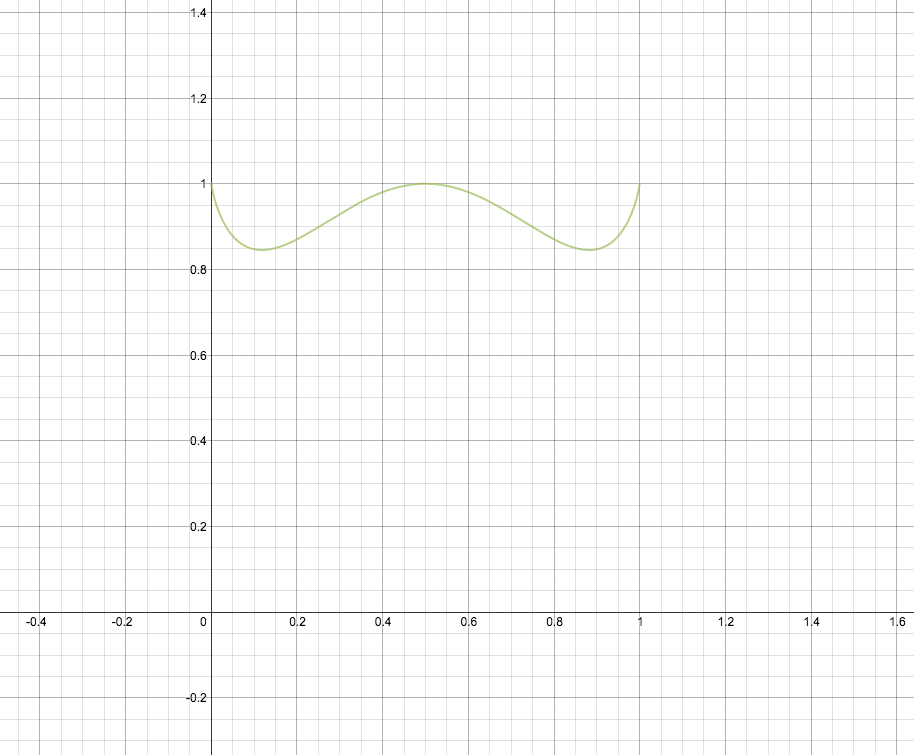
This isn't super rigorous, but here was my intuition and the graph that confirmed it: Let's make a function, f(x) = $x^{1-x}(1-x)^{x} + x^{x}(1-x)^{1-x}$ . f(x) = 1 when x = 0, 1/2, or 1, and plugging into f(x) an x value between 0 and 1/2 or between 1/2 and 1 gives a function value less than 1.

Given that a +b=1

Applying AM greaterthan GM for a^b+b^a we getthe maximum value is 2×ab^(a+b÷2) =2×ab^(1÷2)

and again applyAM greter than GM for a+b=1 we get maximum value is 2×ab^(1÷2)=1 so the maximum value is 1

Weighted AM-GM does the job perfectly $\frac{ba^{(a+b)}+ab^{(a+b)}}{a+b}\geqslant(a^{b(a+b)}b^{a(a+b)})^{\frac{1}{a+b}}=a^{b}b^{a}$ $\frac{aa^{(a+b)}+bb^{(a+b)}}{a+b}\geqslant(a^{a(a+b)}b^{b(a+b)})^{\frac{1}{a+b}}=a^{a}b^{b}$ Add these two, we get $a^{b}b^{a}+a^{a}b^{b}\leqslant a^{a+b}+b^{a+b}=a+b=1$

1) By the AM-GM Inequality $\frac{a+b}{2} \geq \sqrt{ab} => \frac{1}{2} \geq \sqrt{ab}$

Note: $a+b=1 => b=a-1$

$a^bb^a + a^ab^b => a^{a-1}b^a + a^ab^{a-1} => a(\frac{b}{a})^a + b(\frac{a}{b})^a$

2) Again, by AM-GM $a(\frac{b}{a})^a + b(\frac{a}{b})^a\ \geq 2\sqrt{ab}$

Combining (1) & (2)

$a^bb^a + a^ab^b \geq 2(\frac{1}{2}) \geq \fbox{1}$

To make the maximum value of the expression,

in a+b=1 a and b must be 1/2,

because think about what value would give maximum to a*b; 1/4 would be the maximum output by two 1/2.

Thus, plugging 1/2 into the expression of the problem, one gets 1/2 + 1/2,

So the answer is 1.