Mathematical Enigma - XXI
If a rectangle A B C D is inscribed in a semicircle of radius 5 , find the maximum perimeter of the rectangle.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Glad to have a solution from you :)
Sir,can you please attempt my problem named "Global maxima of f(x)".Please post a solution if you get the correct answer,I am unable to solve the question myself.Thanks.
Calc solution which is dumb b/c this is a geo problem.
Let x =length of rectangle and width is √ ( 5 − x 2 ) Perimeter= 2 ∗ x ∗ √ ( 5 − x 2 ) Taking derivative and setting to 0 4 − ( 5 − x 2 ) 2 x , you get x = 2 Thus plugging x = 2 you arrive at perimeter= 1 0
Let the origin be the center of the semicircle. Let (x,y) be the top right corner of the rectangle.
Then perimeter P=4x+2y. For extrema
d
x
d
P
=
4
+
2
∗
d
x
d
y
=
0
,
⟹
d
x
d
y
=
−
2
.
x
2
+
y
2
=
5
,
∴
x
+
y
d
x
d
y
=
0
,
⟹
x
=
2
y
.
∴
t
h
e
s
e
m
i
c
i
r
c
l
e
e
q
u
a
t
i
o
n
,
{
2
y
}
2
+
y
2
=
5
,
i
m
p
l
i
e
s
y
=
±
1
,
s
u
b
s
t
i
t
u
t
i
n
g
,
x
=
±
2
.
Since we can not have y= - 1, and the minimum perimeter is 0, the rectangle with vertices (-2,1),(-2,0),(2,0) and (2,1) gives maximum perimeter which is 1+4+1+4=10.
Let a be the length of the side of rectangle A B C D which lies on the base of the semicircle, b be the length of the side of the rectangle A B C D adjacent to the previously mentioned side and p be the perimeter of rectangle A B C D .
By Cauchy's Inequality:
( 4 a 2 + b 2 ) ( 1 6 + 4 ) ≥ ( 2 a + 2 b ) 2
Note that by Pythagoras' Theorem, we have:
4 a 2 + b 2 = 5
Also,
p = 2 ∗ ( a + b )
So,
5 ∗ 2 0 ≥ p 2
1 0 ≥ p
So the maximum of the perimeter of rectangle A B C D is 1 0 .
Equality when 1 6 4 a 2 = 4 b 2 → a = 4 , b = 1 .
Taking the centre of semicircle as origin we write the polar coordinates same as that of Brian Charlesworth. Since now P =(2×rcosx + rsinx)×2 we have the max of acosy + bsiny as +sqrt(a^2+b^2) Pmax = sqrt(5)×r×2=5×2=10 HENCE PROVED
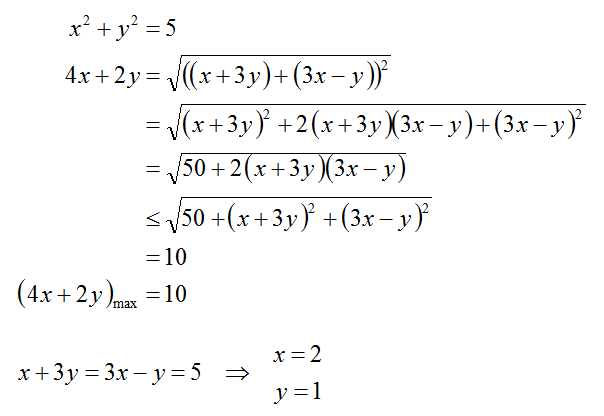
Method 1: For a semicircle of radius r , draw a radial line from its center, (situated at the origin), to a point A on the circle in the first quadrant such that the angle between the x -axis and the radial line is θ > 0 . The coordinates of A are then ( r cos ( θ ) , r sin ( θ ) ) . Going clockwise, the rectangle in question will then have coordinates B ( r cos ( θ ) , 0 ) , C ( − r cos ( θ ) , 0 ) and D ( − r cos ( θ ) , r sin ( θ ) ) .
The perimeter P of rectangle A B C D will then be
P = 4 r cos ( θ ) + 2 r sin ( θ ) = 2 5 r ( 5 2 cos ( θ ) + 5 1 sin ( θ ) ) = 2 5 r sin ( θ + α ) ,
where α = sin − 1 ( 5 2 ) . Choosing θ = 2 π − α allows us to maximize P as 2 5 r , which for r = 5 is 1 0 .
Method 2: Let the coordinates of A this time be ( x , y ) = ( x , r 2 − x 2 ) , since the equation of the semicircle is x 2 + y 2 = r 2 . Then the perimeter P ( x ) will be
P ( x ) = 4 x + 2 y = 4 x + 2 r 2 − x 2 .
Any critical points will occur when d x d P = 4 − r 2 − x 2 2 x = 0
⟹ 4 r 2 − x 2 = 2 x ⟹ 4 ( r 2 − x 2 ) = x 2 ⟹ 4 r 2 = 5 x 2 ⟹ x = 5 2 r ,
for which P = 5 8 r + 2 r 2 − 5 4 r 2 = 5 8 r + 5 2 r = 2 5 r .
As P ( 0 ) = 2 r < 2 5 r we can rest assured that P will achieve a maximum at the critical point x = 2 5 r , which again for r = 5 comes out to 1 0 .