Mathematics of Art

Seven circles, each with radius 1, overlap to form the composite figure shown above. Find the area of the shaded region.
The answer is 6.283.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
Great approach using composite figures to identify the area easily!
This is really smart, how did you come up with that? :O
visually its 1/3 but can you add some logic for it?
outer angle 120 dgree that's the reason to be 1/3?
Just one question: How is the triangle with the curved based a third of a circle? Just trying to make sense out of it myself here
I think Trump has better drawing skills, but I do agree, you're drawings are fantastic!
Shaded area is composed of 6 big pieces + 6 small pieces. You can rotate one of the smaller pieces into the position shown in the picture. Then the shaded area is 1/3 of a circle. There are 6 of them. Thus total shaded area = 2 full circle's area.
That's the approach I took! 👍
I like it, simple but great!
So simple! I blush.
We can clearly see
6
"petals" (inner) and
6
"funnels" (outer). Now,
 Hence, the total area is
2
π
.
Hence, the total area is
2
π
.
Moderator note:
Do you a direct way to show that the areas is exactly equal to 2 circles?
Hint: Connect up a bunch of dots.
The answer comes quick when simplified. Let us call the central circle "circle O, the seventh circle." The other six circles are the symmetrical "petals" of the flower-like figure. If one can calculate the shaded area added by each of the six unit circles remaining, then the total shaded area (call it A) equals six times the shaded area added by each of the six unit circles (call one U and its shaded area S U ).
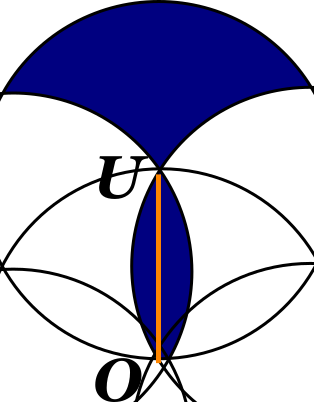
The answer is most visible if one overlays a grid of equilateral triangles. If one uses a segment OU to divide its two adjacent secant arc areas, then it is clear that their positive area matches the two negative areas missing from the remaining shape. If those secant arcs are interchanged, the filled for the empties, then one is left with the filled shape occupying a one-third sweeping arc of the unit circle. A = 6 × S U = 6 × 3 1 π r 2 A = 2 π ≈ 6 . 2 8 3
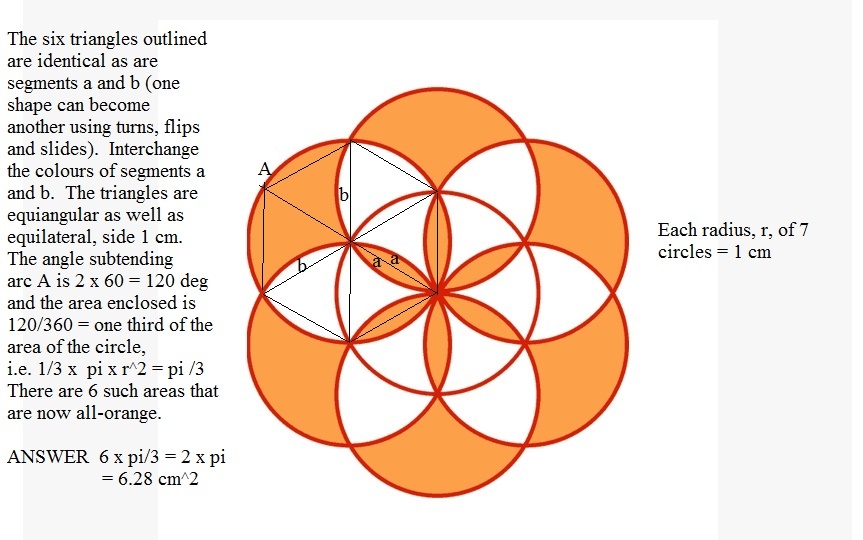
For the inner circle, mark the thin orange slices as "a" and the white pieces as "b".
The single circle, with an area of pi, is 6a + 6b.
Look at the outer orange areas. These are actually made up of one a and two b's. If you total these up, you get 6a + 6a + 12b, which is two circles.
the inner circle gets cut by the outer six circles into six sections, so each of these outer orange areas cuts their respective circle on points that are 120 degrees apart. if these orange areas were straight edged arcs then they would each be 1/3 of the area of a circle. Each of the inner orange petals can fill in one of these orange areas to make a straight edge arc of a circle. There are six outer orange areas and six orange petals, so together they form six arcs of a circle where each arc is 1/3 of a circle. So all together all the orange areas total the area of two circles. Each circle has area one pi. So the answer is 2pi
Since my drawing skills are not as great as some others. I have rendered another's good hand drawn solution as images with MS Paint.
I will also admit that I first solved the problem "the hard way" as follows:
-
Identifying the 1/3 and 1/6 arc chords composed the unshaded areas as area removed from each unit circle.
-
Recalling how areas of sectors and chords can be calculated.
-
Working out value for one circle and adding in the inner petals, that all simplifies down to 2 π
After entering that to earn the right to comment here, I saw the better answer and drew it up for presentation on my own timeline.
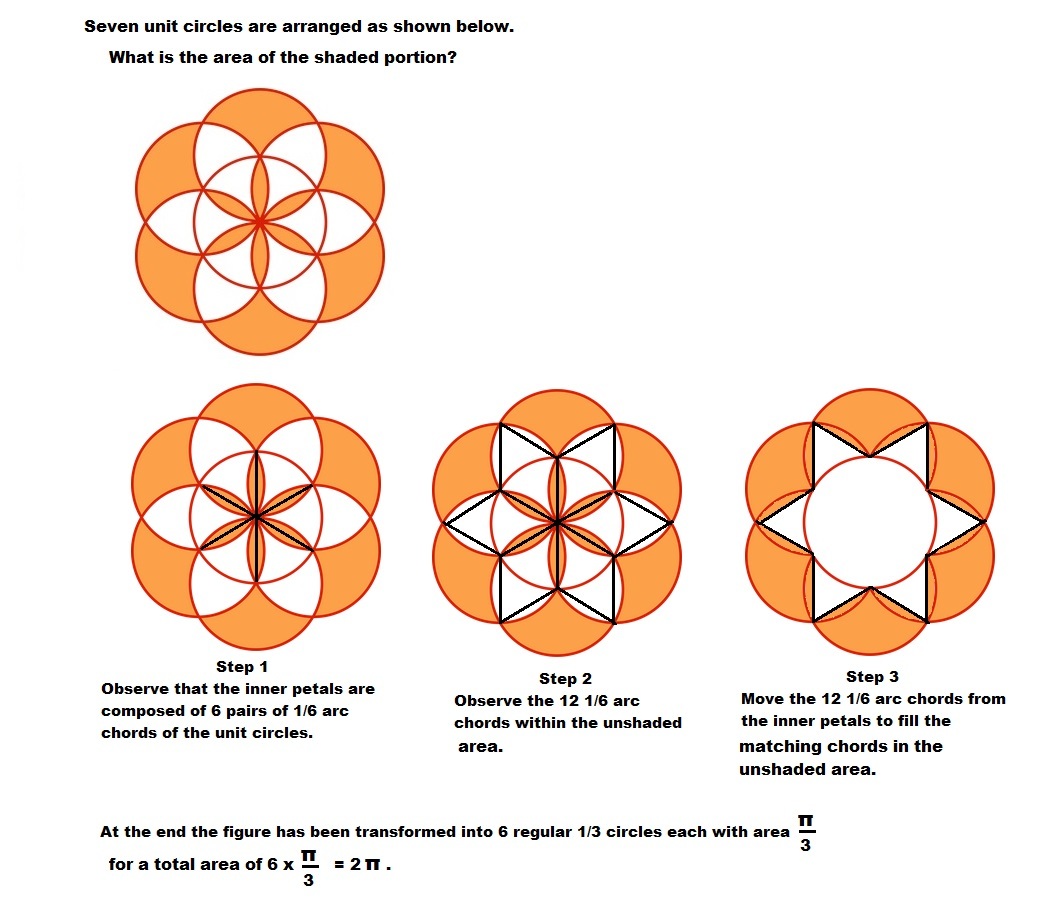
This problem can actually be solved with the brain in a few seconds:
Take a look at the amazing drawing I did since my skills at drawing are so great they are probably the greatest in the world
As you can see in the third panel, the shaded area is made up of six one-thirds of a circle. Therefore, the total area is the area of 2 circles.
So the area is 2 π r 2 = 2 π = 6 . 2 8 . . .