Mathematics Olympics Competition Geometry Problem

Geometry Level 2

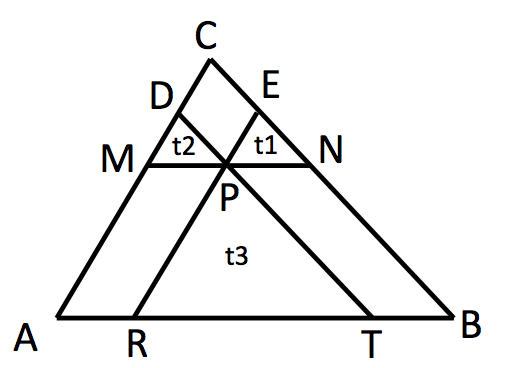$P$ is a point inside of the triangle $ABC$ . $MN \parallel AB$ , $ER \parallel CA$ , $DT \parallel CB$ . The area of triangles $t_1, t_2, t_3$ are $4, 9$ and $49$ . Solve for the area of triangle $ABC$ .

The answer is 144.

3 solutions

Parth Lohomi
Nov 6, 2015

By the transversals that go through $P$ , all four triangles are similar to each other by the $AA$ postulate. Also, note that the length of any one side of the larger triangle is equal to the sum of the sides of each of the corresponding sides on the smaller triangles. We use the identity $K = \dfrac{ab\sin C}{2}$ to show that the areas are proportional (the sides are proportional and the angles are equal) Hence, we can write the lengths of corresponding sides of the triangle as $2x,\ 3x,\ 7x$ . Thus, the corresponding side on the large triangle is $12x$ , and the area of the triangle is

$12^2 = \boxed{144}$

@Parth Lohomi , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.

Brilliant Mathematics Staff - 5 years, 7 months ago

Baby Googa
Mar 9, 2015

All the triangles are all similar.

The ratio of the side lengths of $t3$ and $ABC$ is $\frac{7}{12}$ , so the ratio of their areas is $\frac{49}{144}$ .

So the area of $ABC$ is $144$ .

(This comment has been converted into a solution)

Parth Lohomi - 6 years, 3 months ago

That's exactly how I did it, although Baby Googa's way of doing it is much shorter

Curtis Clement - 6 years, 3 months ago

So, what information told you that there was a 7/12 ratio between t3 and ABC?

Matt Daniels - 6 years, 3 months ago

Try this My 200 followers problem

Nihar Mahajan - 6 years, 3 months ago

The ratio of the side lengths of $t1:t2:t3$ are $2:3:7$ respectively, since the areas are given.

Using the parallel lines given, we can say that $MP \equiv AR$ and $PN \equiv TB$ . So the ratio of $RT$ to $AB$ is $\frac{7}{12}$

Baby Googa - 6 years, 3 months ago

Brilliantly done Baby Googa.. Short and simple.

Bhupendra Jangir - 6 years, 2 months ago

how you came to know that all the three triangles are similar

Deepansh Jindal - 5 years, 2 months ago

Michel Viyella
Jul 18, 2020

t1, t2, t3 and ABC are all similar. The ratio (k) between t1 and t2 is 1.5, and between t1 and t3 is 3.5. By adding AR, RT and TB, we get that 6PN = AB. Therefore, the ratio, k, is equal to 6. Then, the ratio between the areas is k squared, which is 36. Then, 36 x 4 = 144, which is the solution.

Mathematics Olympics Competition Geometry Problem

The answer is 144.

3 solutions

0 pending reports