Math in Origami
Jojo is practicing origami. She folds a square sheet of paper A B C D such that the corner B touches the midpoint of C D . If the crease touches side C B at X , what is the ratio X B C X ?
The answer is 0.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I suppose I should not really comment in the solution of a staff, and I myself use coordinate bashing quite often, but coordinate here seems to be an overkill for the problem here.
Log in to reply
Every solution is a fine solution in my eyes.
Log in to reply
@Andrew Ellinor
Wow, that is nice, because some teachers do not seem to agree with this idea and always insist on a shorter solution.
I myself also appreciate any solution to a problem, and am glad to find that there are people who think alike.
@Dipannita Guhathakurta,
This problem has occurred in the
RMO 1990
paper, problem 3, and it is just a one line application of Pythagoras'.
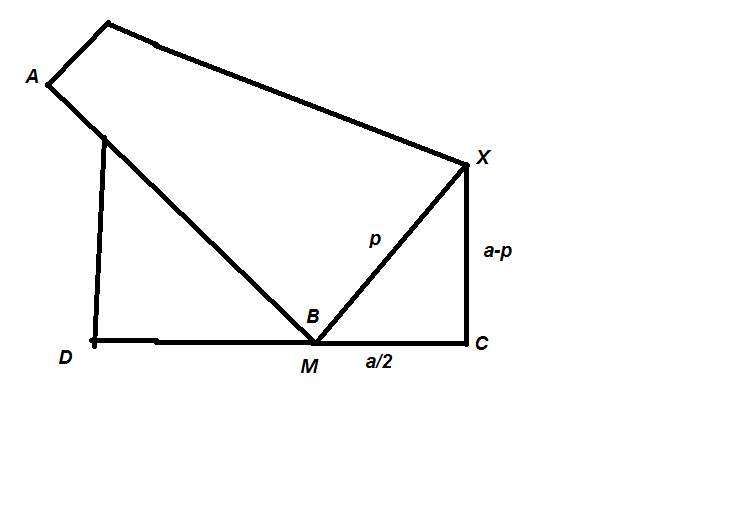 In the figure, apply Pythagoras' in triangle BXC, where we have taken the side of the triangle to be a units long, we find that
p
/
(
a
−
p
)
=5/3 , So if we consider the directed segment BC, the answer would be 5/3, and it would be 3/5 if we consider the directed segment to be CB. So I would request the OP writer to edit the problem.
In the figure, apply Pythagoras' in triangle BXC, where we have taken the side of the triangle to be a units long, we find that
p
/
(
a
−
p
)
=5/3 , So if we consider the directed segment BC, the answer would be 5/3, and it would be 3/5 if we consider the directed segment to be CB. So I would request the OP writer to edit the problem.
P.S. I think I know you.
P.P.S The geometry problem you have posted is a cult problem, and I know the answer to it. I am not telling it here. If you want to talk about it, feel free to mail at [email protected], because I think you have given a wrong answer to it. Just verify once by construction with a protractor and a ruler.
Thanks...it is 5/3. I'd thought it to be CB at first so then the answer will be 3/5.
Log in to reply
Yeah, absolutely.
@Soumava Pal
Thanks. Those who answered 1.66 have been marked correct. I have rephrased the problem and the correct answer is now 0.6.
In future, if you spot an error/ambiguity, please report the problem and we will take the corresponding action.
@Dipanwita Guhathakurta In future, please also edit the question to remove the ambiguity.
Yup it's an easy rmo problem .
Yeah it is. :D
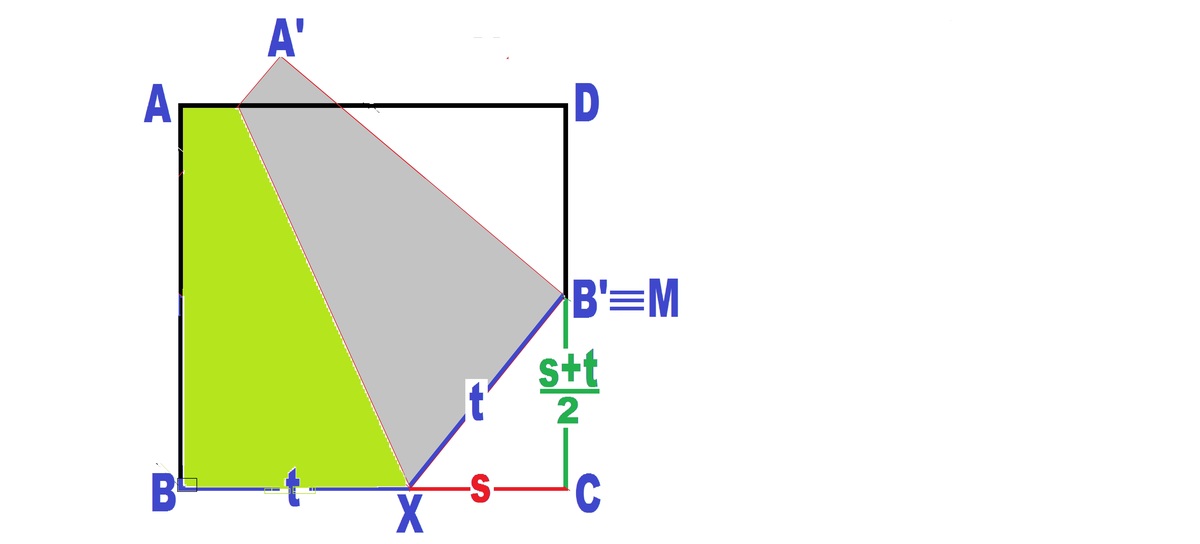 Let XC=s and XB=t. Midpoint of CD be M. Therefore the hypotenuse MX=t , leg MC=
2
s
+
t
and the other leg XC=s.
Let XC=s and XB=t. Midpoint of CD be M. Therefore the hypotenuse MX=t , leg MC=
2
s
+
t
and the other leg XC=s.
∴
t
2
=
(
2
s
+
t
)
2
+
s
2
,
⟹
5
(
t
s
)
2
+
2
t
s
−
3
=
0
.
S
o
l
v
i
n
g
q
u
a
d
r
a
t
i
c
e
q
u
a
t
i
o
n
,
X
B
C
X
=
t
s
=
0
.
6
,
t
a
k
i
n
g
o
n
l
y
t
h
e
p
o
s
i
t
i
v
e
v
a
l
u
e
.
.
We will take the midpoint of C D to be the point M and take the point where the created fold intersects C B to be the point P .
WLOG, take A B = 1 . (Be sure you know why this is retains generality!)
We will consider the general problem of what happens to C B when C M = α . In this problem, we are looking to solve the case where α = 2 1 .
Let the length C P = x .
Knowing ∠ C to be right, we apply the Pythagorean Theorem to △ C M P , giving α 2 + x 2 = ( 1 − x ) 2 .
Expanding and solving, the quadratic term drops out and we get x = 2 1 − α 2 . (Be sure to see this through for yourself!)
Therefore C B is partitioned in a ratio of 1 − 2 1 − α 2 2 1 − α 2 . Rewriting, we have a ratio of 1 + α 2 1 − α 2 . (Again, be sure to see this step through!)
In this case, we have α = 2 1 , so the desired ratio evaluates to 5 3 = 0 . 6 .
Without loss of generality, suppose the side of the square has length 4 with A(0, 4), B(4, 4), C(4, 0), D(0, 0). Let E(2, 0) be the midpoint of CD. The fold is the line over which B will be reflected to obtain E. This line is the perpendicular bisector of BE. To construct the perpendicular bisector of BE, we need the midpoint of BE:
Midpoint of BE: ( 2 2 + 4 , 2 0 + 4 ) = ( 3 , 2 )
Furthermore, we need the slope perpendicular to BE. Since the slope of BE is 4 − 2 4 − 0 = 2 , the perpendicular slope is − 2 1 . Now we can construct the line that forms the crease.
y − 2 = − 2 1 ( x − 3 )
Our interest is X, the point where this line intersects the side BC. Since BC is concurrent with the line x = 4 , we substitute x = 4 into the equation of the crease like so:
y − 2 = − 2 1 ( 4 − 3 ) ⟶ y = 2 3 .
Because BC has length 4, point X splits BC into two segments CX which has length 2 3 and BX which has length 2 5 . The ratio of these lengths is 5 / 2 3 / 2 = 5 3 = 0 . 6 .