Maths Without Number.
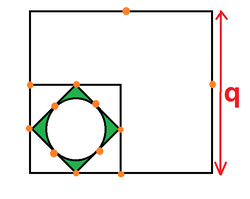 The picture shows 3 quadrilateral and one circle.
-All the quadrilateral are square.
-All the orange dot are midpoint of its respective square.
-The side of the largest square is q.
-Given the area of shaded region (Green) is (3q^2)/[(3L^2) +4].
The picture shows 3 quadrilateral and one circle.
-All the quadrilateral are square.
-All the orange dot are midpoint of its respective square.
-The side of the largest square is q.
-Given the area of shaded region (Green) is (3q^2)/[(3L^2) +4].
Use π = 22/7 , find the value of L.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the areas of the smallest square and the second smallest square be A 1 and A 2 respectively. It is noted that A 1 = 2 1 A 2 . Any the calculations are as follows:
A 1 = A 2 − 4 × the area of corner triangle
= ( 2 q ) 2 − 4 ( 2 1 ) ( 4 q ) 2 = ( 4 1 − 8 1 ) q 2 = 8 1 q 2
The radius of the circle, r = 2 1 ( 4 1 ) ( 2 ) q = 8 2 q
The area of the shaded region,
A = A 1 − π r 2 = 8 1 q 2 − 7 2 2 ( 8 2 q ) 2 = ( 8 1 − 1 1 2 1 1 ) q 2 = ( 1 1 2 1 4 − 1 1 ) q 2 = 1 1 2 3 q 2
⇒ 3 L 2 + 4 = 1 1 2 ⇒ L = 3 1 1 2 − 4 = 3 1 0 8 = 3 6 = 6