Matrix Median Mystery
For any △ A B C , if the median through ∠ A is m 1 , the median through ∠ B is m 2 , and the median through ∠ C is m 3 , then
⎣ ⎡ a 2 b 2 c 2 ⎦ ⎤ = M ⋅ ⎣ ⎡ m 1 2 m 2 2 m 3 2 ⎦ ⎤
for a certain 3 × 3 matrix M .
Find the sum of all the elements of matrix M .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
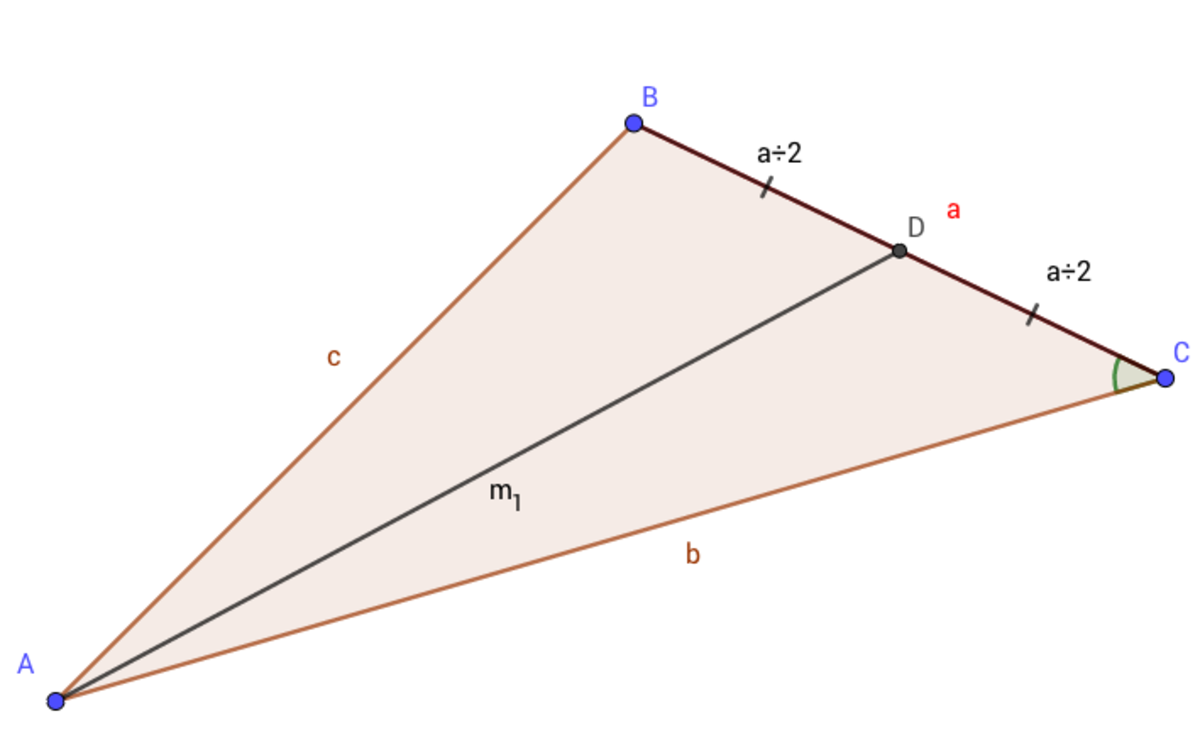 using the laws of cosine:
m
1
2
=
(
2
a
)
2
+
b
2
−
2
2
a
b
cos
(
C
)
=
4
a
2
+
b
2
−
a
b
(
2
a
b
a
2
+
b
2
−
c
2
)
=
4
1
(
−
a
2
+
2
b
2
+
2
c
2
)
→
[
m
1
2
]
=
4
1
[
−
1
2
2
]
⎣
⎢
⎡
a
2
b
2
c
2
⎦
⎥
⎤
→
⎣
⎢
⎡
m
1
2
m
2
2
m
3
2
⎦
⎥
⎤
=
4
1
⎣
⎢
⎡
−
1
2
2
2
−
1
2
2
2
−
1
⎦
⎥
⎤
⎣
⎢
⎡
a
2
b
2
c
2
⎦
⎥
⎤
where the symmetry of
(
m
1
,
m
2
,
m
3
)
to
(
a
,
b
,
c
)
was used to figure out the entire matrix from just one row, we inver this matrix to get
⎣
⎢
⎡
a
2
b
2
c
2
⎦
⎥
⎤
=
9
4
⎣
⎢
⎡
−
1
2
2
2
−
1
2
2
2
−
1
⎦
⎥
⎤
⎣
⎢
⎡
m
1
2
m
2
2
m
3
2
⎦
⎥
⎤
using the laws of cosine:
m
1
2
=
(
2
a
)
2
+
b
2
−
2
2
a
b
cos
(
C
)
=
4
a
2
+
b
2
−
a
b
(
2
a
b
a
2
+
b
2
−
c
2
)
=
4
1
(
−
a
2
+
2
b
2
+
2
c
2
)
→
[
m
1
2
]
=
4
1
[
−
1
2
2
]
⎣
⎢
⎡
a
2
b
2
c
2
⎦
⎥
⎤
→
⎣
⎢
⎡
m
1
2
m
2
2
m
3
2
⎦
⎥
⎤
=
4
1
⎣
⎢
⎡
−
1
2
2
2
−
1
2
2
2
−
1
⎦
⎥
⎤
⎣
⎢
⎡
a
2
b
2
c
2
⎦
⎥
⎤
where the symmetry of
(
m
1
,
m
2
,
m
3
)
to
(
a
,
b
,
c
)
was used to figure out the entire matrix from just one row, we inver this matrix to get
⎣
⎢
⎡
a
2
b
2
c
2
⎦
⎥
⎤
=
9
4
⎣
⎢
⎡
−
1
2
2
2
−
1
2
2
2
−
1
⎦
⎥
⎤
⎣
⎢
⎡
m
1
2
m
2
2
m
3
2
⎦
⎥
⎤
Great solution!
Of course, given the existence of M , we can apply the result to an equilateral triangle. All three sides have length u , and all three medians have length 2 1 u 3 , and then 3 u 2 = a 2 + b 2 + c 2 = ( 1 1 1 ) M ⎝ ⎛ m a 2 m b 2 m c 2 ⎠ ⎞ = ( 1 1 1 ) M ⎝ ⎛ 1 1 1 ⎠ ⎞ 4 3 u 2 = X × 4 3 u 2 where X is the sum of the entries in M , so that X = 4 .
Note that M*[1, 1, 1] will equal to a 3x1 matrix, [a^2, b^2, c^2], in which each element in row i equals the sum of the entries in row i of M. So if we find a^2, b^2, and c^2 for which triangle ABC has medians of length 1, then a^2+b^2+c^2 is our answer. Since all of the medians are equal, you can safely assume that ABC is an equilateral triangle. Some basic geometry gives a = b = c = 2/sqrt(3) and the answer would be 4/3+4/3+4/3=4