Matrixes

Over the complex numbers, if $A$ has distinct eigenvalues, it is diagonalizable. Since $sin A$ is a convergent power series in $A$ , eigenvectors of $A$ are also eigenvectors of $sin A$ , so $A$ having distinct eigenvalues would imply that $sin A$ is diagonalizable. Since $\begin{pmatrix} 1 & 1996 \\ 0 & 1 \\ \end{pmatrix}$ is not diagonalizable, it can be $sin A$ only for a matrix $A$ with equal eigenvalues. This matrix can be conjugated into the form $\begin{pmatrix} x & y \\ 0 & x \\ \end{pmatrix}$ for some x and y. Using the power series for sin, we compute -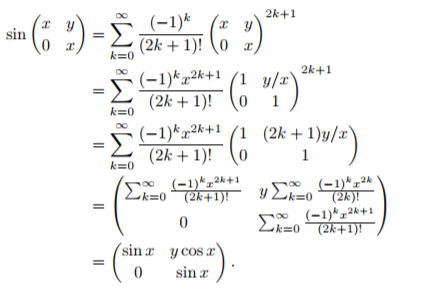 Thus if $sin (x) = 1$ , then $cos (x) = 0$ and $sin \begin{pmatrix} x & y \\ 0 & x \\ \end{pmatrix}$ is the identity matrix. In other words, $sin A$ cannot equal a matrix whose eigenvalues are $1$ but which is not the identity matrix. Therefore, no such matrix $A$ exists.