Max Power (2-20-2021)

Electricity and Magnetism Level 3

An AC voltage source has internal voltage $V_S$ and internal impedance $Z_S$ . A load resistor $R$ is connected across the source terminals. What value of $R$ maximizes the average power dissipated in the load resistor?

Bonus: Is there anything interesting about the optimal $R$ value?

Details and Assumptions:
1) $V_S = 10 + j 0$
2) $Z_S = 1 + j 2$
3) $j = \sqrt{-1}$

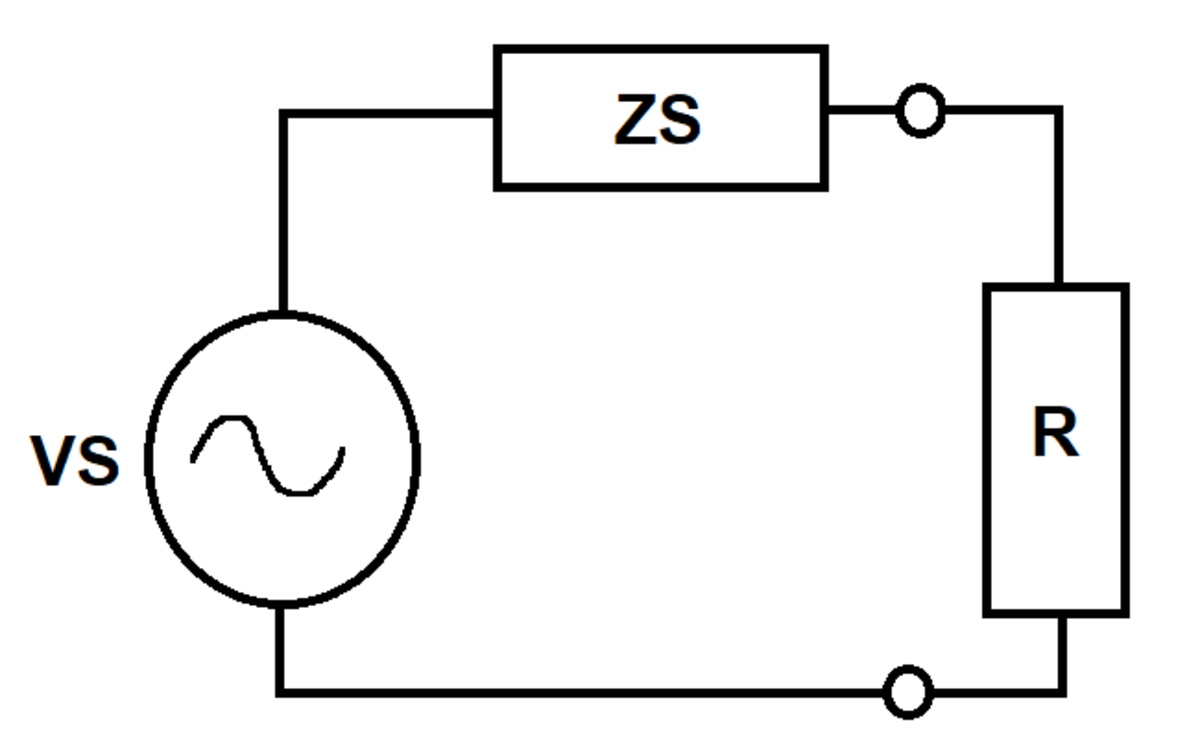
The answer is 2.236.

1 solution

Karan Chatrath
Feb 21, 2021

$I = \frac{V_S}{Z_S+R}$ $\implies P = (IR)I^{*}$ Plugging in values and simplifying leads to:

$P = \frac{100R}{(1+R)^2 + 4}$

To find the value of $R$ that maximises $P$ , we need to ensure that the following two conditions are satisfied at the optimal point:

$\frac{dP}{dR}=-\dfrac{100\left(R^2-5\right)}{\left(R^2+2R+5\right)^2}=0$ $\frac{d^2P}{dR^2}= \dfrac{200\left(x^3-15x-10\right)}{\left(x^2+2x+5\right)^3} \biggr \rvert_{R=R_{\mathrm{optimal}}} <0$

Leaving out simplififications, the optimal value of $R$ is $\boxed{R_{\mathrm{optimal}} = \sqrt{5}}$

As for the bonus question, I do notice that the optimal value of $R$ corresponds to the modulus of the impedance $Z_S$ . I don't see what this means physically.

In DC circuits with a source resistance and a load resistance, the load consumes maximum power when the two resistors have the same value. A similar concept applies in this problem, except that we're just matching the absolute values since that is the most we can do. If we could have a complex load impedance $Z_L$ , the max load power would occur when $Z_L$ is the complex conjugate of $Z_S$ .

Steven Chase - 3 months, 2 weeks ago

Max Power (2-20-2021)

The answer is 2.236.

1 solution

0 pending reports