Max power with variation
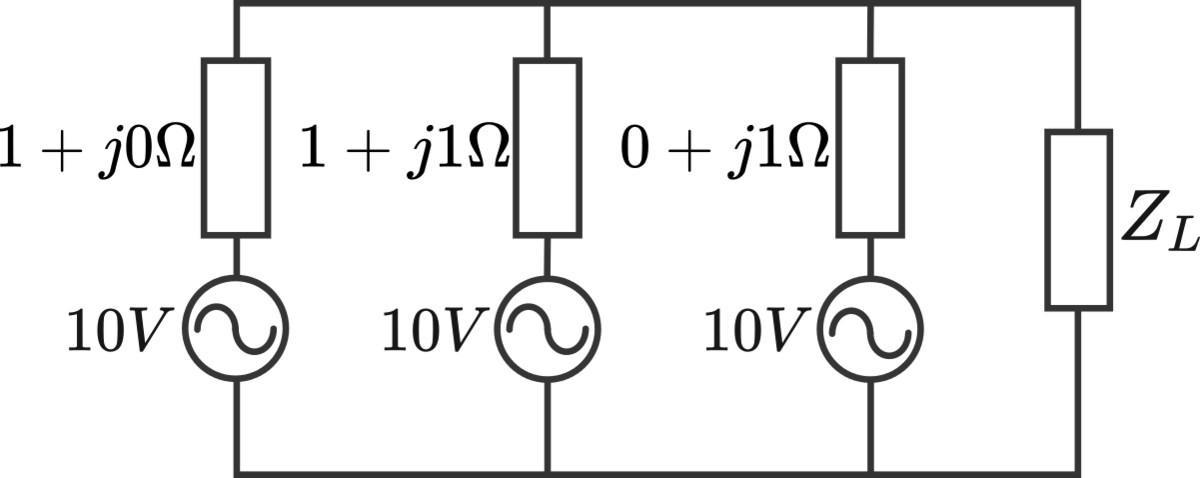 Consider the AC circuit shown above, with source impedances and RMS source voltages given. The load impedance internally consists of a combination of resistors, capacitors, and inductors. What is the maximum active power (in watts) which can possibly be dissipated by the load?
Consider the AC circuit shown above, with source impedances and RMS source voltages given. The load impedance internally consists of a combination of resistors, capacitors, and inductors. What is the maximum active power (in watts) which can possibly be dissipated by the load?
Here is the twist: the voltage source in the middle is running in opposite phase ( off) relative to the other two sources, which are in phase with each other.
This problem is based on Steven Chase's problem with a similar title.
HINT: Use Kirchhoff's laws to deduce a simple equivalent circuit, consisting of one voltage source and one impedance..
The answer is 8.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We will use Z 1 = 1 , Z 2 = 1 + j and Z 3 = j (all in units of Ω ). The current in the first branch is I 1 , in the second branch I 2 and in the third branch I 3 , all pointing up. The current in the load is I , pointing down. The voltage sources are V 1 = V 0 , V 2 = − V 0 and V 3 = V 0 , where V 0 = 1 0 V and the negative sign of V 2 represent the 1 8 0 o phase difference.
Kirchhoff's junction law will be
I = I 1 + I 2 + I 3 .
We write down three loop laws, each one including one of the voltage sources, the corresponding impedance and the load:
V 0 − I 1 Z 1 − I Z = 0
− V 0 − I 2 Z 2 − I Z = 0
V 0 − I 3 Z 3 − I Z = 0 .
Using these equations we express the three branch currents in terms of I and plug them into the junction law:
I = Z 1 V 0 − I Z + Z 2 − V 0 − I Z + Z 3 V 0 − I Z
and we solve this to the current:
I = V 0 1 + Z ( 1 / Z 1 + 1 / Z 2 + 1 / Z 3 ) 1 / Z 1 − 1 / Z 2 + 1 / Z 3 .
It is helpful to re-write this as
I = V 0 1 / Z 1 + 1 / Z 2 + 1 / Z 3 1 / Z 1 − 1 / Z 2 + 1 / Z 3 Z + 1 / Z 1 + 1 / Z 2 + 1 / Z 3 1 1 = V ′ / ( Z + Z 0 ) ,
where V ′ = V 0 1 / Z 1 + 1 / Z 2 + 1 / Z 3 1 / Z 1 − 1 / Z 2 + 1 / Z 3 and Z 0 = 1 / Z 1 + 1 / Z 2 + 1 / Z 3 1 .
The expressions above show that the circuit driving the load can be replaced with a a single voltage source of V ′ and and internal impedance of Z 0 . Note that in the case when there is no phase difference the negative sign of the Z 2 term turns to positive, and we get back to original problem by Steven Chase.
Working with the values given for the impedances we get
1 / Z 1 + 1 / Z 2 + 1 / Z 3 1 / Z 1 − 1 / Z 2 + 1 / Z 3 = 1 + 1 / ( 1 + j ) + 1 / j 1 − 1 / ( 1 + j ) + 1 / = j ( 1 + j ) + j + 1 + j j ( 1 + j ) − j + 1 + j = 3 j j = 1 / 3 .
Interestingly, this number is real, although with other choice of parameters it could be complex as well. The real number means that in our case the effective voltage source is in phase with the voltage sources in the first and third branches. Furthermore,
Z 0 = 1 + 1 / ( ! + j ) + 1 / j 1 = j ( 1 + j ) + j + 1 + j j ( 1 + j ) = ( 1 + j ) / 3
For the maximum power the load impedance has to be the complex conjugate of the internal impedance Z L = ( 1 − j ) / 3 . It follows that the total impedance is real, R t o t = Z 0 + Z L = 2 / 3 . The total power dissipated in the circuit is P = ∣ V ′ ∣ 2 / R t o t . Half of this power is dissipated on the external load (the other half is dissipated on the internal impedance). The result is
P = 2 1 R t o t ∣ V ′ ∣ 2 = ( 1 / 2 ) ( 1 0 / 3 ) 2 ( 3 / 2 ) = 8 . 3 3 W