Maxima in tube
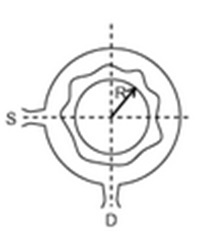 A narrow tube is bent in the form of a circle of radius
as shown Two small holes
are made in the tube at positions right angle to each other. A source placed at
generated a wave of intensity
which is equally divided into two parts. One part travels along the longer path while the other travels along the shorter path. Both the waves meet the point
where a detector is placed.
A narrow tube is bent in the form of a circle of radius
as shown Two small holes
are made in the tube at positions right angle to each other. A source placed at
generated a wave of intensity
which is equally divided into two parts. One part travels along the longer path while the other travels along the shorter path. Both the waves meet the point
where a detector is placed.
If maxima is found at the detector then, the magnitude of wavelength cannot be
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For a maxima at D , path difference Δ x = n λ
2 3 π R − 2 π R = n λ
⇒ λ = n π R
λ = π R , 2 π R , 3 π R , 4 π R , e t c .