Maximal Aquarium
What is the height for the maximum volume of John's
open topped
aquarium where the surface area is
4
0
0
cm
2
assuming that it has a square base
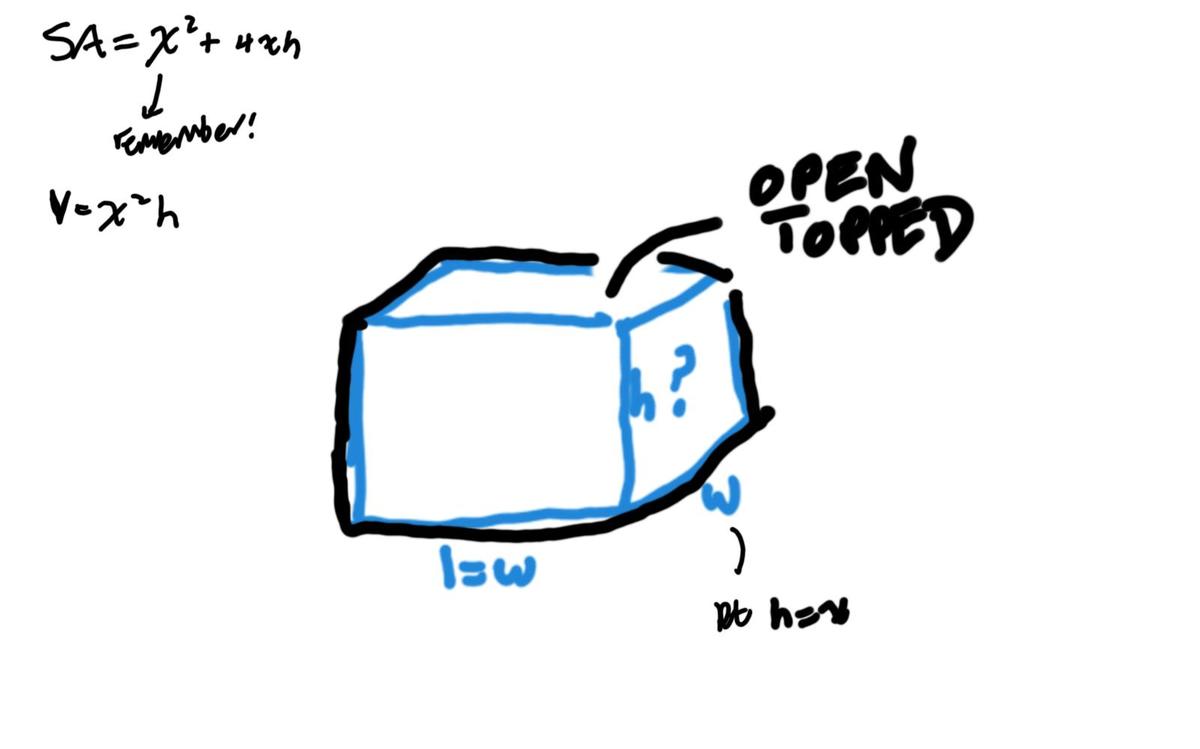 hint: the illustration confuses the variables!
hint: the illustration confuses the variables!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Very interesting, I like it!
V = w 2 h
A = w 2 + 4 w h ⇒ h = 4 w A − w 2 Substitute this expression for h into the expression for V : V = w 4 A − w 2 Now set d w d V = 0 to get w = 3 A leading to h = 1 2 A = 3 1 0 3 , which I did not immediately find among the answers. But it is the same answer in a simpler form.
Let the width be x and height be h (I'd like to see a solution with h=x), SA = x^2 + 4xh. We already know that the surface area is 400 cm^2 so then we shall solve for h
-
400 = x^2+4xh
-
4 x 4 0 0 − x 2 = h
Now that we have solved for the height in terms of the width it is time to use the volume equation.
-
V = x^2*h
-
V = x^2*( 4 x 4 0 0 − x 2 )
-
V = 4 4 0 0 x − x 3
Now we solve for the derivatives
-
V' = 1/4(400-3x^2)
-
V" = 1/4(-6x)
We see that the volume is concave down for all positive x Now lets solve for the critical points of the volume
-
V' = (400-3x^2)/4 = 0
-
400-3x^2 = 0
-
400=3x^2
-
x^2=400/3
So now we know that x is the positive or negative (for our purposes it is positive) square root of 400/3
If we use the height equation
- 4 x 4 0 0 − x 2 = h
400-400/3 / 80/sqrt(3)
400sqrt(3) - 400sqrt(3)/3 / 80
h=5sqrt(3) - 5sqrt(3)/3
Let the width of the square base be w and the height of the aquarium by h . Then its volume is given by V = w 2 h and its surface area
4 w h + w 2 4 w 2 h + w 3 4 V + w 3 4 d w d V + 3 w 2 = 4 0 0 = 4 0 0 w = 4 0 0 w = 4 0 0 Multiply both sides by w Note that V = w 2 h Differentiate both sides w.r.t. w .
We note that d w d V = 0 , when w = 3 2 0 and d w d 2 V < 0 . This means V is maximum when w = 3 2 0 . From
4 w h + w 2 4 ( 3 2 0 ) h + ( 3 2 0 ) 2 3 h + 3 5 ⟹ h = 4 0 0 = 4 0 0 = 5 = 5 3 − 3 5 3