Maximal Quadrangle
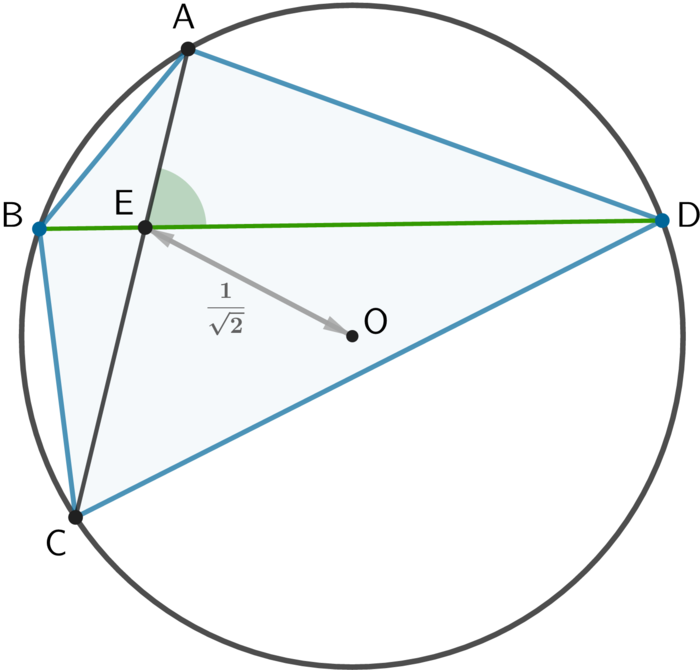 A quadrilateral
A
B
C
D
is inscribed in a
unit
circle such that the diagonal
A
C
is fixed. The point of intersection of the diagonals is also fixed
2
1
units away from the center of the circle. Now, the diagonal
B
D
is varied to maximize the area of the quadrilateral. Note that depending on the position of the fixed diagonal
A
C
, different maximal quadrilaterals will be generated.
A quadrilateral
A
B
C
D
is inscribed in a
unit
circle such that the diagonal
A
C
is fixed. The point of intersection of the diagonals is also fixed
2
1
units away from the center of the circle. Now, the diagonal
B
D
is varied to maximize the area of the quadrilateral. Note that depending on the position of the fixed diagonal
A
C
, different maximal quadrilaterals will be generated.
In this familiy of maximal quadrilaterals, find the area of the quadrilateral which has the minimum angle between its diagonals. The answer is w u v for coprime integers u , v , w . Submit u + v + w .
The answer is 61.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
How did you solve d m d ( tan θ ) = 0 ? It seems to me that the resulting expression will be huge and very hard to work with.
Log in to reply
I simplified the expression to tan θ = m 3 1 ( m 2 + 1 − 1 ) 3 1 + m ( m 2 + 1 − 1 ) 3 2 − m 3 5 ( m 2 + 1 − 1 ) 3 2 − m 3 2 − m 3 4 ( m 2 + 1 − 1 ) 3 1 , and then used wolframalpha to find that the minimum was at m = 5 2 . (Click on "use the real-valued root instead" and then on "exact form". It got too complicated for me to do by hand.)
Rotate the diagram and place on the coordinate plane so that E is at the origin and O is at ( 2 1 , 0 ) .
The unit circle will then have the equation ( x − 2 1 ) 2 + y 2 = 1 .
Let the line through A C have the equation y = m x and the line through B D have the equation y = n x . Without loss of generality, let n > m .
As the intersections of ( x − 2 1 ) 2 + y 2 = 1 and y = m x , A and C have the coordinates of A ( 2 ( m 2 + 1 ) 1 − m 2 + 2 , 2 ( m 2 + 1 ) m ( 1 − m 2 + 2 ) ) and C ( 2 ( m 2 + 1 ) 1 + m 2 + 2 , 2 ( m 2 + 1 ) m ( 1 + m 2 + 2 ) ) .
Likewise, B and D have the coordinates of B ( 2 ( n 2 + 1 ) 1 − n 2 + 2 , 2 ( n 2 + 1 ) n ( 1 − n 2 + 2 ) ) and D ( 2 ( n 2 + 1 ) 1 + n 2 + 2 , 2 ( n 2 + 1 ) n ( 1 + n 2 + 2 ) ) .
The area of △ A E D is A △ A E D = 2 1 ∣ E A x ⋅ E D y − E D x ⋅ E A y ∣ = 2 1 ∣ ∣ ∣ ∣ ∣ 2 ( m 2 + 1 ) 1 − m 2 + 2 ⋅ 2 ( n 2 + 1 ) n ( 1 + n 2 + 2 ) − 2 ( n 2 + 1 ) 1 + n 2 + 2 ⋅ 2 ( m 2 + 1 ) m ( 1 − m 2 + 2 ) ∣ ∣ ∣ ∣ ∣ = 4 ( m 2 + 1 ) ( n 2 + 1 ) ( n − m ) ( m 2 + 2 − 1 ) ( n 2 + 2 + 1 ) .
Likewise, the area of the other triangles are A △ D E C = 4 ( m 2 + 1 ) ( n 2 + 1 ) ( n − m ) ( m 2 + 2 + 1 ) ( n 2 + 2 + 1 ) , A △ B E C = 4 ( m 2 + 1 ) ( n 2 + 1 ) ( n − m ) ( m 2 + 2 + 1 ) ( n 2 + 2 − 1 ) , and A △ A E B = 4 ( m 2 + 1 ) ( n 2 + 1 ) ( n − m ) ( m 2 + 2 − 1 ) ( n 2 + 2 − 1 ) .
The area of quadrilateral A B C D is then A A B C D = A △ A E D + A △ D E C + A △ B E C + A △ A E B = ( m 2 + 1 ) ( n 2 + 1 ) ( n − m ) m 2 + 2 n 2 + 2 .
The maximum area of quadrilateral A B C D for a given m -value will be when d n d A A B C D = n 2 + 2 ( m 2 + 1 ) ( n 2 + 1 ) 2 m 2 + 2 ( m n 3 + 3 m n + 2 ) = 0 , or when m n 3 + 3 m n + 2 = 0 , which is when n = 3 m ( m 2 + 1 − 1 ) 3 ( m 2 + 1 − 1 ) 2 − 3 m 2 .
The angle between y = m x and y = n x is tan θ = 1 + m n n − m , which has a minimum for m < 0 when d m d ( tan θ ) = 0 , which after substituting n = 3 m ( m 2 + 1 − 1 ) 3 ( m 2 + 1 − 1 ) 2 − 3 m 2 solves to m = − 5 2 .
If m = − 5 2 , then n = 3 m ( m 2 + 1 − 1 ) 3 ( m 2 + 1 − 1 ) 2 − 3 m 2 = 3 ( − 5 2 ) ( ( − 5 2 ) 2 + 1 − 1 ) 3 ( ( − 5 2 ) 2 + 1 − 1 ) 2 − 3 ( − 5 2 ) 2 = 2 , and the area of the quadrilateral is A A B C D = ( m 2 + 1 ) ( n 2 + 1 ) ( n − m ) m 2 + 2 n 2 + 2 = ( ( − 5 2 ) 2 + 1 ) ( ( 2 ) 2 + 1 ) ( 2 + 5 2 ) ( − 5 2 ) 2 + 2 ( 2 ) 2 + 2 = 2 7 8 2 6 .
Therefore, u = 8 , v = 2 6 , w = 2 7 , and u + v + w = 6 1 .