Maximally Acute Decagon
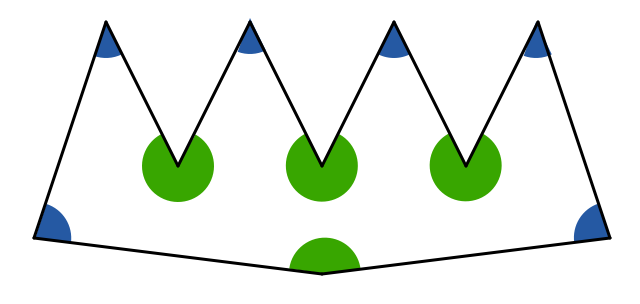
In a simple decagon (10-sided polygon with no self-intersections), what is the maximum number of internal angles that could be acute?
For example, the above image shows 6 acute angles, marked in blue.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the number of acute angles be A . Then, the number of non-actue angles is 1 0 − A .
Consider the sum of these angles. We have:
8 × 1 8 0 ∘ = ∑ internal angles < A × 9 0 ∘ + ( 1 0 − A ) × 3 6 0 ∘
This in turn gives us A < 8 . Since A is an integer, thus 7 is an upper bound.
It remains to show that 7 can indeed be achieved. I got this by starting out with making the acute angles close to (but just below) 90, and making the non-actue angles close to 360.
There is quite a lot of leeway in the inequality, since 7 × 9 0 ∘ + 3 × 3 6 0 ∘ = 1 7 1 0 ∘ vs 8 × 1 8 0 ∘ = 1 4 4 0 ∘ . So, there should be a lot of possible (and nicer) diagrams.