Maximization of Hemisphere Inscribed Cylinder Volume
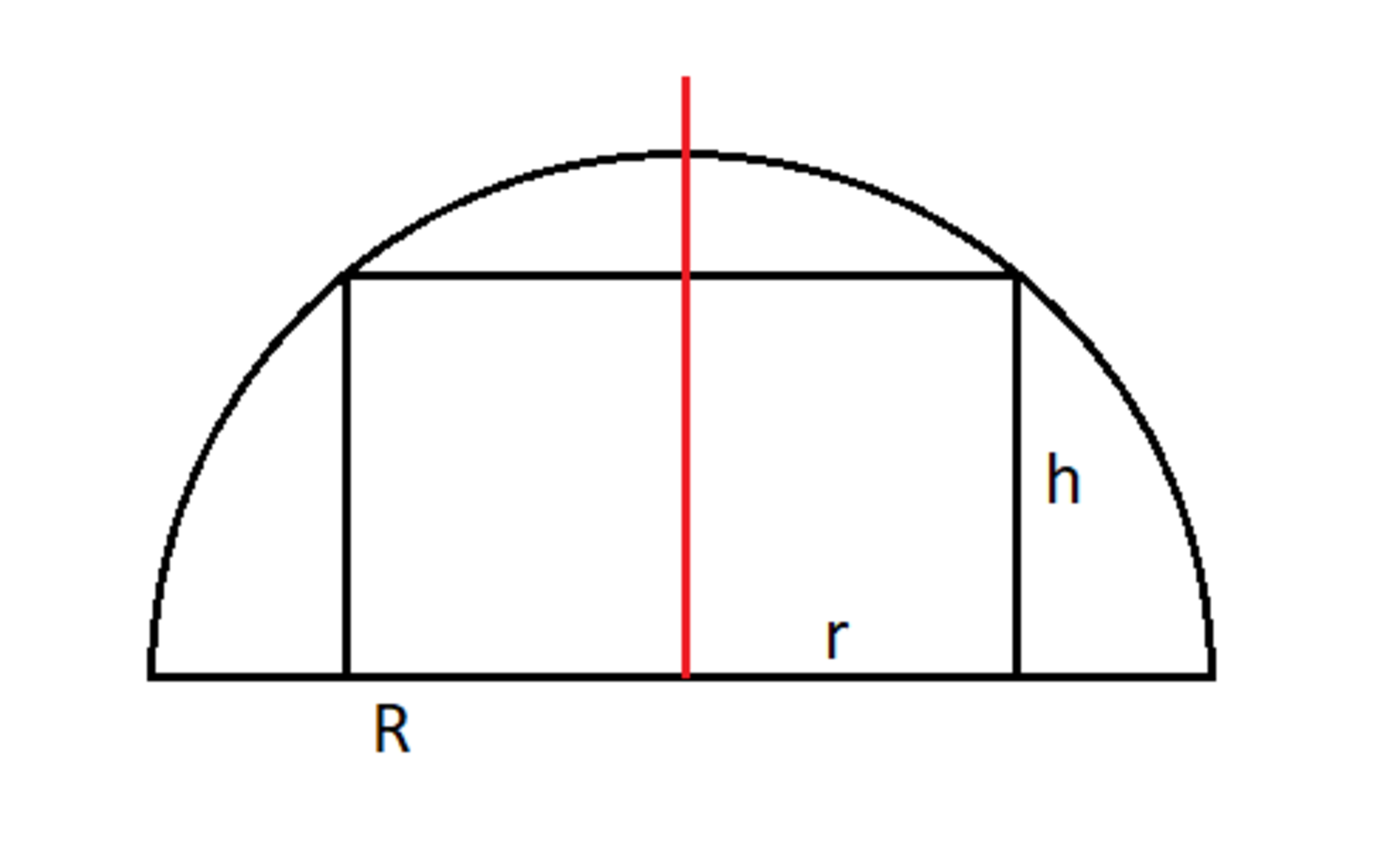
Given a hemisphere of radius , you inscribe a cylinder inside it such that the cylinder and the hemisphere share the same axis of symmetry. The figure below shows the cross-section of the hemisphere-cylinder. Find the cylinder of maximum possible volume. If the ratio of the maximum cylinder volume to the volume of the hemisphere is , then enter as your answer.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius and height of the cylinder be r and h respectively. We note that r 2 = R 2 − h 2 and the volume of the cylinder is:
V V ( h ) d h d V ( h ) ⟹ h = π r 2 h = π h ( R 2 − h 2 ) = π ( R 2 − 3 h 2 ) = 3 R Differentiate both sides w.r.t. h Equating it to zero Since h > 0
Since d h 2 d 2 V ( h ) < 0 for h > 0 , V ( 3 R ) = 3 3 2 R 3 is the maximum cylinder volume. The volume of the hemisphere is 3 2 π R 3 . Therefore the required ratio is 3 3 2 π R 3 × 2 π R 3 3 = 3 1 , ⟹ n = 3 .