Maximize Euler
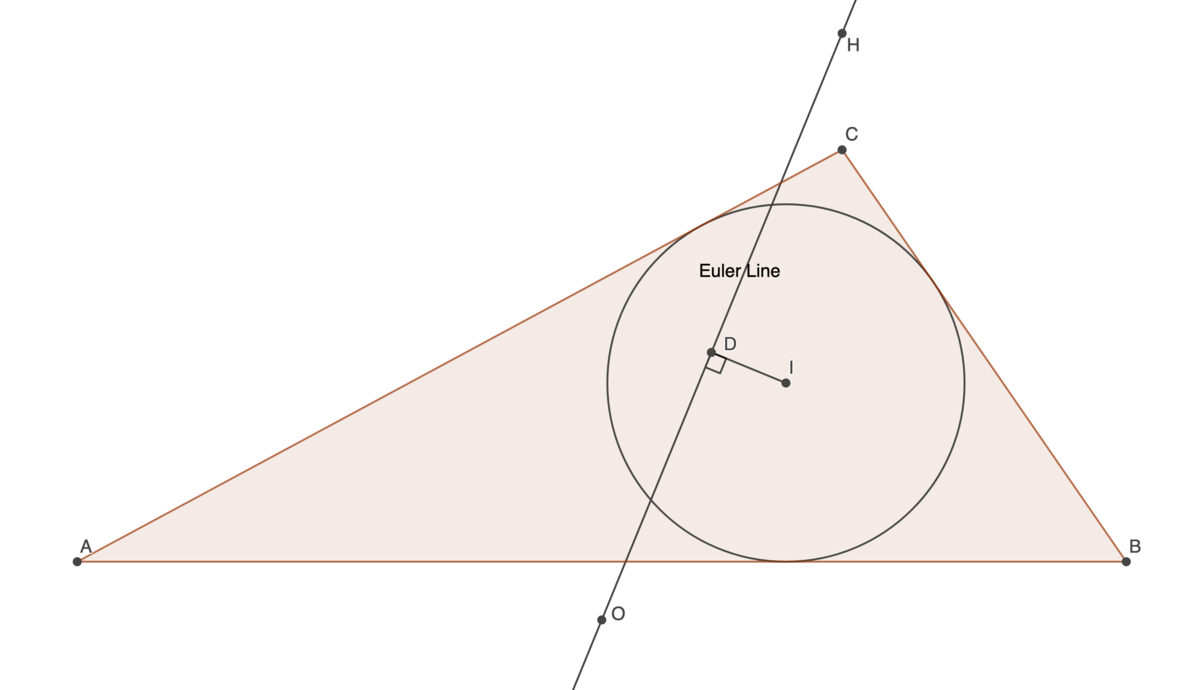
Given a triangle of an area of 11 and a perimeter of 16, find the maximum perpendicular distance between the incenter and the Euler line .
For example, if were such a triangle (where represent the circumcenter , orthocenter , and incenter , respectively), find the largest possible value of .
The answer is 0.247944.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If a triangle's incentre lies on its Euler line, it must be isosceles (and vice-versa); so in a sense this problem is asking for the "most scalene" triangle with perimeter 1 6 and area 1 1 .
I didn't get very far analytically (but would be interested if someone did); the basis of my numerical approach was as follows:
Call the triangle's area T and its semiperimeter s . Let its sidelengths be a , b , c (as usual opposite vertices A , B , C respectively).
We know T and s ; let's make a a parameter. By definition, b + c = 2 s − a
Now, from Heron's formula, s ( s − a ) ( s − b ) ( s − c ) s ( s − a ) ( s 2 − ( b + c ) s + b c ) s ( s − a ) ( s 2 − ( 2 s − a ) s + b c ) s ( s − a ) ( b c − s ( s − a ) ) b c = T 2 = T 2 = T 2 = T 2 = s ( s − a ) + s ( s − a ) T 2
Knowing b + c and b c means we can find b and c as the roots of a quadratic (up to a choice of sign).
We also have T = r s and 4 R T = a b c where r and R are the inradius and circumradius respectively. So r = s T , R = 4 T a b c
Now, it's possible to proceed in a few ways. We can embed everything in a Cartesian coordinate system (which works but is messy); we can use trilinear coordinates to find the distance between the incentre and the Euler line (this involves a lot of trig); or we can try to stick with geometry as long as possible.
Recall the Euler line goes through the circumcentre O and the centroid G . We want the distance to the incentre I . With a bit of internet based research, we can find the following: O I = R ( R − 2 r ) , G I = 3 1 5 r 2 − 1 6 R r + s 2 , G O = R 2 − 9 1 ( a 2 + b 2 + c 2 )
ie we have all the sidelengths of the triangle Δ I G O in terms of quantities we've already found; and the distance we want is the altitude of this triangle from I .
I didn't fancy the algebra here so just proceeded numerically (from the above we can try values of a and calculate the distance); I used a golden section search to find the maximum distance, which came out to be 0 . 2 7 9 4 … when the sides of the triangle were approximately 3 . 9 7 3 4 , 5 . 5 7 6 6 , 6 . 4 5 0 0 ) .
Bonus question (although, really, it's the original question again): in what way is this the most scalene triangle satisfying the conditions? Is there some simple geometric intuition here?