Maximize Sugar Cubes

Computer Science Level 1

An ant climbing down an ant-hill can choose to go either down and to the right or down and to the left at each level until it reaches the bottom of the hill. And at each junction, the ant collects a number of sugar grains indicated by the numbers in the circle.

Being greedy, this ant believes that if it always moves down towards the larger of the two values directly below, it will be able to collect the largest number of sugar grains overall. With the hill as shown above, is this greedy strategy optimal for collecting sugar?

Yes, being greedy is optimal No, it is not

Agnishom Chattopadhyay by Agnishom Chattopadhyay , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Ojasee Duble
Mar 10, 2017

If the ant follows the caves that has the larger of the two sugar cubes then,

The ant may get 3 + 2 + 6 + 2 = 13 sugar cubes

Whereas, there is another path available where the ant can get 3 + 1 + 6. + 9 = 19 sugar cubes

Hence, what ant believes is false

17 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

A "reverse greedy" approach gets an optimal amount of sugar here; start at 9, which is the biggest endpoint, go back to 6 (which is the largest previous step) then back to 1 (which is the only previous step) then back to 3 (which is the only previous step).

Is this always the case? What would you need to change to foil both the regular greedy and reverse greedy approaches?

How would one arrive at the better path given the entire ant hill?

Agnishom Chattopadhyay - 4 years, 3 months ago

Log in to reply

The idea is to work backwards. From bottom to top, you calculate each position the largest amount of sugar grains the ant can find. In the process, you can easily find the best path by looking at its two children.

For example,

  • at depth 4 you can have maximum 1, 2, 9, 3 sugar grains.
  • at depth 3 you can have maximum 6 + 2 (going right) = 8, 4 + 9 (going right) = 13, 6 + 9 (going left) = 15.
  • at depth 2 you can have maximum 2 + 13 (going right) = 15, 1 + 15 (going right) = 16.
  • at depth 1 you can have maximum 3 + 16 (going right) = 19.

Christopher Boo - 4 years, 2 months ago
Annie Li
Mar 19, 2017

When you look at the bottom line, you will realise that 9 is the biggest number. since 6 and 4 is on top of 9 you will have to decide on the bigger number. Obviously 6 is bigger so therefore the ant should travel 3 then 1 then 6 then 9

12 Helpful 0 Interesting 0 Brilliant 0 Confused

Yes, this is a very good way to solve such problems. This would work for an arbitrarily large hill.

Agnishom Chattopadhyay - 4 years, 2 months ago

thanks Agnishom Chattopadhyay

Annie Li - 4 years, 2 months ago

Also, what does arbitrarily mean

Annie Li - 4 years, 2 months ago

Log in to reply

Arbitrarily large means as large as you want.

Please do not go posting comments asking people to follow you. One way to gain more followers is to post more problems and/or solutions and get noticed.

Agnishom Chattopadhyay - 4 years, 2 months ago
Stewart Gordon
Mar 26, 2017

You can find the optimal path systematically as follows. From each node in the penultimate row, eliminate the arrow that leads to the lower number. And then add to the number in said node the number in the node that the remaining arrow from that node leads to.

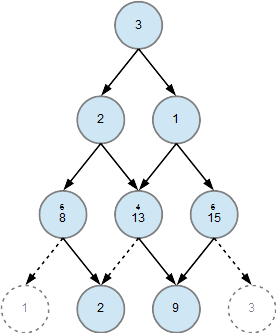
And then repeat the process with the next row of arrows upwards

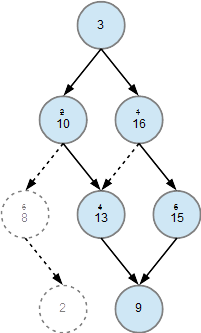
and finally with the arrows from the root node, and then you have the optimal path.

5 Helpful 0 Interesting 0 Brilliant 0 Confused

This is an informative solution! Essentially, we are breaking the problem into subproblems that are easier to solve and later combine them to get the final answer. This useful technique is called Dynamic Programming .

Christopher Boo - 4 years, 2 months ago

Nice! Only the last image has wrong numbers in 2nd row. Left node should read "small 2, big 15", right one should read "small 1, big 16".

Martin Ramsch - 3 years, 4 months ago

Log in to reply

Agreed, the left node should have a 15. The right node is as you say though. The small numbers are struck through, to represent the replacement of them with the big number as part of my algorithm.

Stewart Gordon - 3 years, 4 months ago

Log in to reply

Ah, I misread the small struck through 1 as "4". Thanks for pointing out!

Martin Ramsch - 3 years, 4 months ago
Kelsey Goroncy
Mar 24, 2017

First, let's consider the case where the ant is greedy. The path for that is 3>2>6>2, which yields 13 sugar grains. Now, notice that there is a 9 in Level 4. The two paths leading to the 9 are a 4 and 6, which yields a minimum of 13 grains between Level 3 and Level 4 if the ant finishes at the 9. Given that all values are positive integers, we can stop at this point because we know that any path leading to the 9 will yield more than 13 sugar grains and thus will surpass the number of sugar grains that the ant would obtain through the greedy approach.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Yes, this is indeed a valid observation. So, the ant could definitely do better than greedy if he had large scale information about the hill.

Agnishom Chattopadhyay - 4 years, 2 months ago

If the ant can see the entire hill, then the top-down greedy strategy shown is not the best strategy - one that works around attempting to link the highest numbers at each stage, or a bottom-up greedy strategy, would be better. For this hill, it certainly does not yield the optimal result for the ant.

However, that makes the assumption that the ant can see the whole hill. With no information other than the two paths available at the next stage, what is the best strategy? The obvious answer would be to collect the maximum number available.

Does this strategy hold, however, if backtracking is allowed? Unlimited backtracking would allow the ant to either carry all the sugar in the hill or gain knowledge of the entire hill, rendering the limitation moot. However, if an additional resource was factored in - time - how would the strategies change? How is it different if the paths are all of the same length, or of different lengths? How does it change if we assume the ant moves more slowly if it is carrying more sugar? Or, alternatively, a limit on the allowed number of backtracks; is it better to look into the next stage of the hill on the side with more or less sugar if you cannot revisit the first path you search? Or perhaps a better strategy is to be greedy for one or two turns, which (depending on the rules of the limitation) may allow the ant to backtrack with ease through the last part of the hill?

The question itself is not very challenging, but it makes me wonder about how the strategies for other variations of the problem would differ from the original.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Yes, these are interesting alternatives to consider. It's worth brainstorming and creating problems about them.

Agnishom Chattopadhyay - 4 years, 2 months ago

being greedy is optimal most of the time.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Not really. If the ant did not have information about the entire hill, being greedy is the best he could do. But if he did, then it is possible to do better, right?

Agnishom Chattopadhyay - 4 years, 2 months ago

As example demonstrate this assumption is incorrect.

Lukasz Bonenberg - 4 years, 2 months ago

I'd be interested in what model of number distribution would support such a statement. (I don't mean that sarcastically.)

Richard Desper - 4 years, 2 months ago

Log in to reply

With all due respect, I don't think the solution author really thought this through.

Agnishom Chattopadhyay - 4 years, 2 months ago

Oh this is a nice follow up question, how do you propose that we begin to work on this?

Pi Han Goh - 4 years, 2 months ago

What does optimal mean?

Annie Li - 4 years, 2 months ago

Log in to reply

A strategy is optimal if it maximizes the utility. Here, the ant is doing optimal if it can get the highest number of sugar cubes.

Agnishom Chattopadhyay - 4 years, 2 months ago

This answer is wrong. With the hill as shown above, is this greedy strategy optimal for collecting sugar? The question specifically asks about strategy, not outcome. The ant made the right strategic choice in each case. Generate the numbers randomly, and the right strategy is the greedy strategy. This "hill" is an anecdotal demonstration of a specific event. If the question were, "With the hill as shown above, does the ant collect more sugar than an ant using the opposite strategy," then the answer would be the ant using the improper strategy collected more sugar. I single anecdote does not however verify the optimal strategy. The question/answer is linguistically/philosophically/statistically inaccurate. In other words it is wrong. The question was written by someone with undetermined mathematical skills, but with definite lacking in language, philosophy, and thought. Or, to put it more completely, one has to shut off the brain, and not evaluate the question, to get the answer "correct".

Wayne Moore - 4 years, 2 months ago

Just to clear issues; the ant doesn't know the outcome of any side it takes until it takes it. Always going for the larger value will yield 13 cubes while always going for the smaller value will yield 10 cubes. That is given the ant can only do one or the other but not both.

Michael Owen Otieno - 4 years, 2 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...