Maximize the Area

Consider the following circle diagram of $\overline{AC}$ and $\overline{BD}$ being diameters and central point $O$ included within quadrilateral $ABCD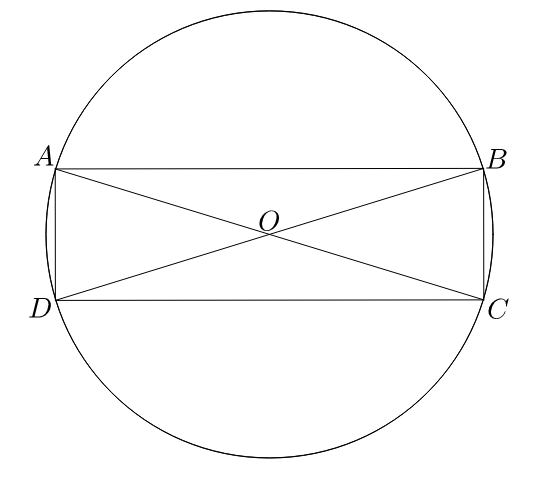$ : For a convex quadrilateral to have the maximum area, it is concyclic (inscribed inside a circle), where the sum of each pair of opposite angles is $180^{\circ}$ . Since quadrilateral $ABCD$ is cyclic, both fixed diagonals $\overline{AC}$ and $\overline{BD}$ touch the circumference of the circle, which implies that they are both same diameters of the circle (otherwise, see Remark ). Since $O$ is the midpoint of both $AC$ and $BD$ , $|AO| = |BO| = |DO| = |CO| = 0.5$ . Noting that $\overline{AB} \parallel \overline{CD}$ and $\overline{BC} \parallel \overline{AD}$ , we can conclude that the inscribed quadrilateral is a rectangle.

Remark: Suppose the shape is not a rectangle. Then, it is a different convex quadrilateral. If we were to drag one of the diagonals away from the midpoint, then the shape is not cyclic. Because $|AC| = |BD|$ , at least one of either endpoints of the diagonals leaves the circle by dragging the diagonal away from the center.

Let $s_1$ and $s_2$ denote the length of $\overline{AB}$ and $\overline{BC}$ , respectively. The perimeter of the rectangle is $2\left(s_1 + s_2\right) = \dfrac{5}{2}$ which is equivalent to $s_1 + s_2 = \dfrac{5}{4}$ By Pythagorean Theorem , $\begin{array}{rl} \left(s_1\right)^2 + \left(s_2\right)^2 = 1 \end{array}$ We want to maximize $s_1s_2$ , the area of the rectangle. With some algebra, the result is $\begin{array}{rl} \left(s_1 + s_2\right)^2 &= \dfrac{25}{16}\\ \left(s_1\right)^2 + \left(s_2\right)^2 + 2s_1s_2 &= \dfrac{25}{16}\\ 1 + 2s_1s_2 &= \dfrac{25}{16}\\ 2s_1s_2 &= \dfrac{9}{16}\\ s_1s_2 &= \boxed{\dfrac{9}{32}} \end{array}$ where $p + q = 9 + 32 = \boxed{41}$ .

Same as the solution of Michael Huang.
$Since ~the~diagonals~are~equal,~the ~maximum~area~will~be~for~a~rectangle.\\ Let~a,b~be~the~sides.\\ \therefore~a^2+b^2=1,~~but~a+b=\frac 1 2*\frac 5 2 =\frac 5 4.\\ \implies~a^2+2ab+b^2=\dfrac{25} {16}.~\\ \therefore~2ab=\dfrac{25} {16}-1=C.\\ So~area=ab=\dfrac{9} {32}=\dfrac{p} {q}.\\ p+q=\Large \color{#D61F06}{41}.$