Maximize The Area
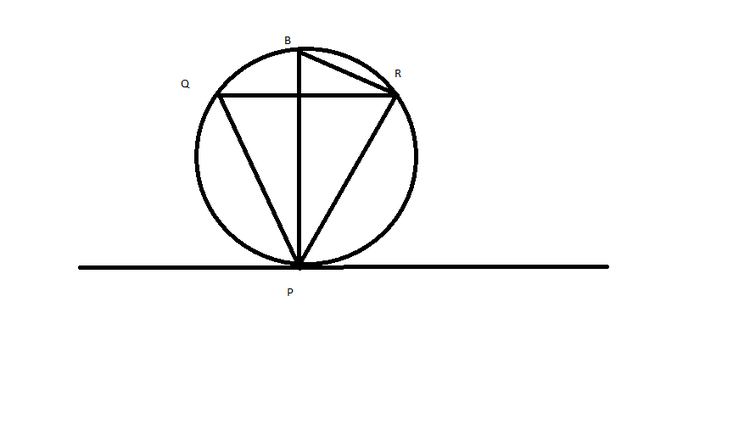 The point
P
is given on the circumference of a circle of radius 10
c
m
.
, and the chord
Q
R
is parallel to the tangent touching the circle at point
P
. What is the maximum possible area of
△
P
Q
R
in
c
m
.
2
?
The point
P
is given on the circumference of a circle of radius 10
c
m
.
, and the chord
Q
R
is parallel to the tangent touching the circle at point
P
. What is the maximum possible area of
△
P
Q
R
in
c
m
.
2
?
The answer is 129.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
i did it like this. , since we had to found largest area so its height must be also the maximum possible and so the maximum possible height as 15 using the property of circles. and then by using pythagorous theorem found out qr. and found the area. is that not one of the metho
Log in to reply
Will you please explain " the maximum possible and so the maximum possible height as 15 using the property of circles".
what u did was partially correct, h m a x can b greater than 15 but in that case the base will correspondingly reduce, and hence the resultant area will reduce. we need to prove the fact that an equilateral triangle wil have max. area for a circle with a given radius.
Largest area must be an equilateral triangle. So put R=10 in 0.75 x s q r t 3 x R 2 and get the value, ie 129.903
Congrats. Short and sweet.
VERY SIMPLE ... a largest area trianle inside a circle is an equilateral trianle.... so consider PQR AS AN equilateral trianle nd solve ....bingo
Think that, BP and QR intersects at D \ and O is the centre of the circle.\ Add O,R and O,Q\ now DR= 1 0 2 − ( 1 0 − B D ) 2 = 2 0 . B D − B D 2 \ ∴ QR=2 2 0 . B D − B D 2 \ and DP=20-BD\ ∴ the area of triangle △ PQR= 2 1 × 2 2 0 . B D − B D 2 × ( 2 0 − B D ) \ Now the maximum result is for BD=5, which is "129.9038"
cause QR is parallel to the tangent at P and < angle QOR = x (O is center of circle), so we can get : \n
< QOP = < ROP = (360 - x)/2 = 180 - x/2
Area of triangle PQR :
= 1/2
QO
RO
sin(< QOR) + 1/2
QO
PO
sin(< QOP) + 1/2
PO
RO
sin(< ROP)
= 1/2
10
10
sin(x) + 1/2
10
10
sin(180-x/2) + 1/2
10
10
sin(180-x/2)
= 50
sin(x) + 100
sin(x/2)
define the area of triangle PQR in f(x) = 50
sin(x) + 100
sin(x/2)
to get maximum of a function f(x) , f'(x)=0 :
f(x) = 50
sin(x) + 100
sin(x/2)
f'(x) = 0
50
cos(x) + 50
cos(x/2) = 0
known that cos(x/2) = sqrt((1+cos(x))/2) so
cos(x) = -sqrt((1+cos(x))/2)
2
cos^2(x)-cos(x)-1 = 0
(2
cos(x)+1)(cos(x)-1) = 0
x = {0 , 2
pi/3 , 5
pi/3}
the reasonable value of x is 2
pi/3, so
f(2
pi/3) = 50
sin(2
pi/3) + 100 sin(pi/3) = 75*sqrt(3) = 129.9038
^^V
(1) Take the chord at x from the centre. Hence the expression for the Area is as follows.
(2) The height of the triangle H = 10 + x. The (base/2)^2 = (chord length/2)^2 = 10^2 - x^2..
(3) (Area)^2 = (1/2)^2
(10^2 - x^2.)
( 10 + x )^2.
(4) Differentiating w.r.t. x and setting to zero, we get x =5.
{Note that max for area is the same as max for (Area)^2 . I have used this method so the differentiation is easy.}.
(5) H= 10 + 5 = 15;.... base/2 = sqrt( 10^2 - 5^2) = 5(sqrt3)....Area = 129.90.
I give this as another method. Ashu Dablo's is the best method.
I may also mention that given a parameter of a rectangle, square has the max area. Given the total surface area, cube has the max volume. For and open top box, given cardboard area, max. volume is obtain with square base and height = half of the length of the square side. Given surface area of ellipsoid, sphere has max volume. And so on, symmetry gives max. min.
Let H = P B ∩ Q R , P H = x . The second Euclid's theorem yields Q H 2 = P H ⋅ H B = x ( 2 0 − x ) Therefore [ P Q R ] = P H ⋅ Q H = x x ( 2 0 − x ) Using AM-GM inequality we get [ P Q R ] = x 3 ( 2 0 − x ) = 3 3 3 x ⋅ 3 x ⋅ 3 x ⋅ ( x − 2 0 ) ≤ 3 3 ( 4 2 0 ) 4 = 7 5 3 = 1 2 9 . 9 0 4 The maximum is attained when x = 1 5 .