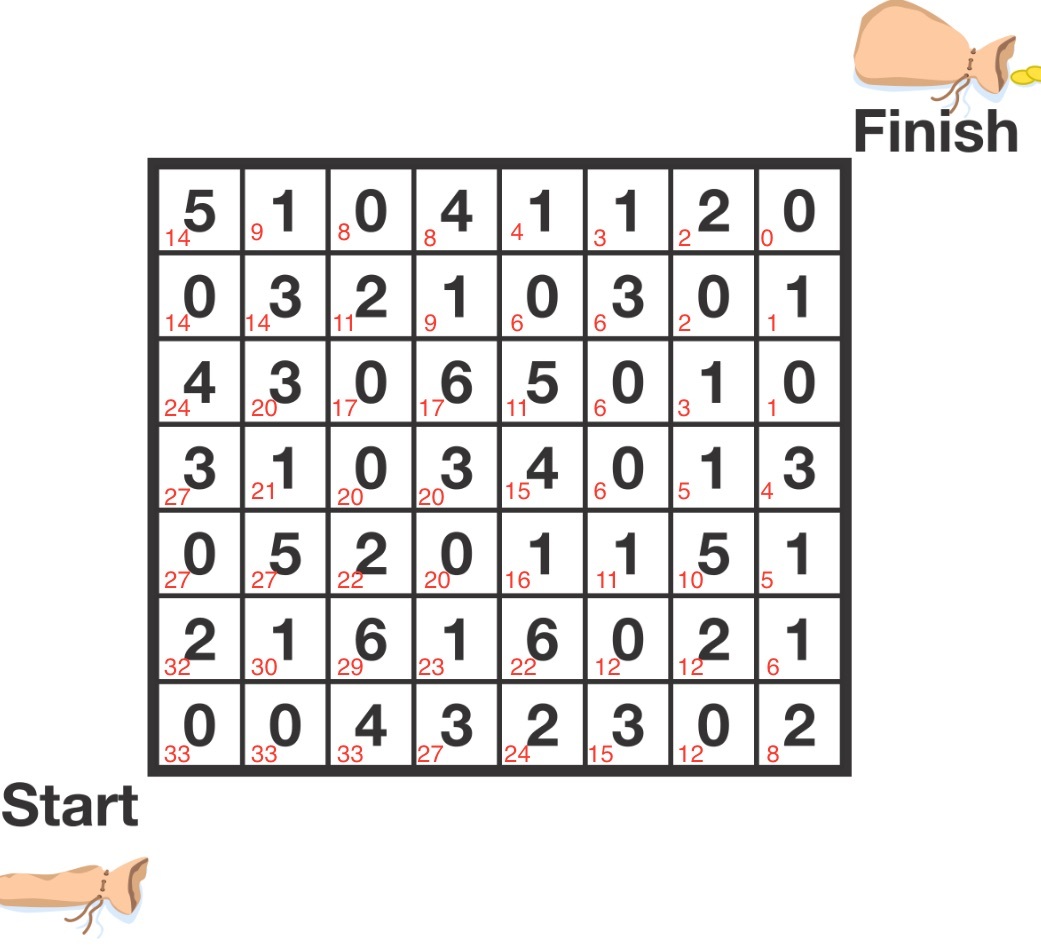
Maximize the Gold

Relevant wiki: Dynamic Programming

The Key to find the answer here is that , if you want to know the max number of coins to reach cell (i,j) then you can compute it recursively by knowing the no max coins to reach cell(i+1,j) and cell(i,j-1) ( assuming Adam starts from bottom left and goes to top right). Recursively:
Let $F(i,j)$ be the function that gives max number of coins to reach cell (i,j) then, $F(i,j) = max(F(i+1,j) ,F(i,j-1)) + coins(i,j)$ Giving the answer to be $33$ Using DP can help avoid recalculate already calculated values and solve in $\mathcal{O}(n*m)$ Time Complexity ( where $m,n$ are rows and columns ) Hence Line 19 may be: (Note that the code has been written by taking rows and columns from topleft and so the condition has been modified accordingly!)

1

max_coins[(column,row)] = max(max_coins[(column-1,row)],max_coins[(column,row-1)]) + coins[(column,row)] 

Relevant wiki: Dynamic Programming

Solved with a spreadsheet (LibreOffice Calc).

Placed the numbers as shown on the A1..H7 grid.

In the cell J7 I placed the formula =MAX(I7,J8)+A7 and copied it to the J1..Q7 grid.

The result was in the cell Q1.

If you are interested in these problems have a look at the literature on Operational Research.

Relevant wiki: Dynamic Programming

I think it is a bit self explanatory, but anyway, let me explain:

The idea to get rid of the corners is not to define coordinates at -1, as this is ugly and quite a messy workaround. Instead, a function filters valid coordinates to retrieve from max_coins. Better yet would be to instead write a recursive function that would not even try values smaller than 0, but as Python is not tail-call optmized I don't think it would be very performant.

Then, to unravel the path, the concept is a lot similar from the one used in generating the max_coins list: just look from where there are the most coins and append it.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

from brilliant import goldgrid
coins = goldgrid.grid()
height, width = goldgrid.height(coins), goldgrid.width(coins)

#Initializing the dictionary for the maximum coins up to a certain cell

max_coins = {(0,0): coins[0,0]}

def get_max_coins(coord):
    if coord[0] >= 0 and coord[1] >= 0:
        return max_coins[coord]
    else:
        return 0

for row in range(height):
    for column in range(width):
        if not (column, row) == (0,0):
            left_coin = get_max_coins((column - 1, row))
            down_coin = get_max_coins((column, row - 1))

            max_coins[(column,row)] = max(left_coin, down_coin) + coins[column,row]


def trace_path(coord, accumulator):
    accumulator.append(coord)

    left_coord = (coord[0] - 1, coord[1])
    down_coord = (coord[0], coord[1] - 1)

    max_coord = (left_coord, down_coord)[get_max_coins(down_coord) > get_max_coins(left_coord)]

    if coord != (0,0):
        return trace_path(max_coord, accumulator)
    else:
        return accumulator

#Print path and maximum value
print(trace_path((width - 1, height - 1), []))
print(get_max_coins((width - 1, height - 1)))

Here is my solution:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

    from brilliant import goldgrid
    coins = goldgrid.grid()
    height, width = goldgrid.height(coins), goldgrid.width(coins)

    #Initializing the dictionary, including making edges exist but undesirable
    max_coins = {(-1,n) : 0 for n in range(0,height)}
    max_coins.update({(n,-1) : 0 for n in range(0,width)})

    #Using recursion / dynamic programming to find the remaining maximums
    for row in range(0,height):
        for column in range(0,width):
                max_coins[(column,row)] = max(max_coins[(column,row-1)], max_coins[(column-1,row)]) + coins[(column,row)]

    #Print the maximum value for the top right cell
    print(max_coins[(width-1,height-1)])

    #Initializing the path list
    path = []
    #Starting at the top right, descend backwards
    current_row = height-1
    current_column = width-1
    #Note there will be 14 moves in total
    for move in range(0,14):
        path.append((current_column,current_row))
        if max_coins[(current_column-1,current_row)] >= max_coins[(current_column,current_row-1)]:
            current_column -= 1
        else:
            current_row -= 1
    #Reverse the path to start it from the bottom left
    path.reverse()
    #Print the path taken
    print(path)

On closely examining the grid, you will notice that the grid has 6 only three times, out of which you can go through any two. You just have to now pick up the path that gives you the max. sum. The grid is so arranged that it supports this logic.

from brilliant import goldgrid
...
...
for column in range(1,width):
if max coins[(column-1,row)]> max coins[(column,row-1)]:
max coins[(column,row)] = max coins[(column-1,row)]+coins[(column,row)];
else:
max coins[(column,row)] = max coins[(column,row-1)]+coins[(column,row)];
..
print(max_coins[(width-1,height-1)])