Maximizing Range 2
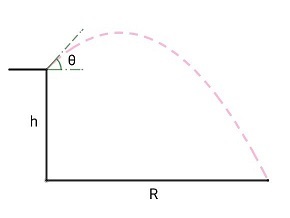
A projectile is fired from a height , as shown in the figure, with an initial velocity at an angle of inclination from the horizontal. Determine in degrees so that the range of the projectile, measured on the ground, is maximum.
Details and Assumptions
- .
- Neglect air resistance.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The trajectory of the particle is x = v t cos θ y = h + v t sin θ − 2 1 g t 2 or y = h + x tan θ − 2 v 2 g x 2 sec 2 θ and so the particle hits the ground when h + x tan θ − 2 v 2 g x 2 sec 2 θ = 0 . Thus the range x is maximized when x ′ ( θ ) = 0 , and we see that x ′ tan θ + x sec 2 θ − v 2 g x x ′ sec 2 θ − v 2 g x 2 sec 2 θ tan θ ( tan θ − v 2 g x sec 2 θ ) x ′ = 0 = x sec 2 θ ( v 2 g x tan θ − 1 ) and so maximum range is achieved when v 2 g x tan θ = 1 , and hence h + g v 2 − 2 v 2 g ( x 2 + g 2 v 4 ) x 2 = 0 = g 2 v 2 ( v 2 + 2 g h ) Thus the maximum range is g v v 2 + 2 g h , achieved when tan θ = v 2 + 2 g h v . In this case, with v 2 = g h , we have tan θ = 3 1 , and so θ = 3 0 ∘ .