Maximum
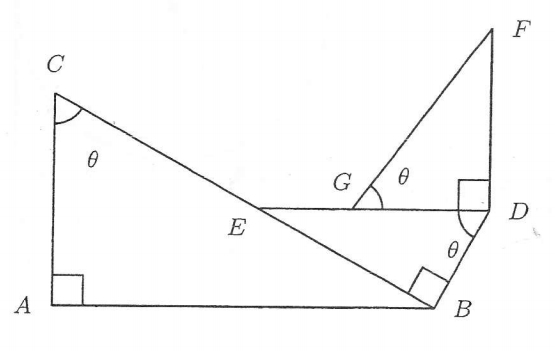
The diagram above shows three right-angled triangles, where B C = 1 4 , G F = 1 0 , D E = 7 and ∠ B C A = ∠ B D E = ∠ F G D = θ .
Find the maximum value of A B + B D + D F .
This is a part of the Set .
The answer is 25.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A B + B D + D F = B C sin θ + D E cos θ + G F sin θ = 1 4 sin θ + 7 cos θ + 1 0 sin θ = 2 4 sin θ + 7 cos θ Note that 7 2 + 2 4 2 = 2 5 2 = 2 5 ( 2 5 2 4 sin θ + 2 5 7 cos θ ) Let tan ϕ = 2 4 7 = 2 5 ( sin θ cos ϕ + sin ϕ cos θ ) = 2 5 sin ( θ + ϕ )
Since maximum of sin ( θ + ϕ ) = 1 , therefore maximum of A B + B D + D F = 2 5 .
Assume the random value of AB+BD+DF is n and the answer is m. Notice that with the given data:
n = A B + B D + D F = 1 4 sin θ + 7 cos θ + 1 0 sin θ = 2 4 sin θ + 7 cos θ = ( 2 4 tan θ + 7 ) cos θ
d θ d n = d θ d ( 2 4 sin θ + 7 cos θ ) = 2 4 cos θ − 7 sin θ
When this first derivative equals zero, since the value of n is upper and lower bounded, then there is a value of θ that maximize the value of n. We get 2 4 cos θ = 7 sin θ , which means tan θ = 7 2 4 and this, with cos 2 θ + sin 2 θ = 1 , results cos θ = ± 2 4 2 + 7 2 7 = ± 2 5 7 . We take the positive value because it makes n positive and thus maximum. Hence:
m = ( 2 4 ( 7 2 4 ) + 7 ) ( 2 5 7 ) = 2 5
We know that A B = 1 4 sin θ
B D = 7 cos θ
D F = 1 0 sin θ
Adding them, we get the desired expression as 2 4 sin θ + 7 cos θ We need to find the maximum of this.
By Cauchy - Swartz, we know that
( 2 4 2 + 7 2 ) ( sin 2 θ + cos 2 θ ) ≥ ( 2 4 sin θ + 7 cos θ ) 2
⟹ 2 5 ≥ 2 4 sin θ + 7 cos θ
Equality holds iff θ = tan − 1 7 2 4
Therefore 2 5 is the maximum.