Maximum and Minimum of Equation

By completing the square,

$y = - [sin x + a/2]^2 + (a^2)/4 + b + 1$

Let $sin x$ be -1 and 1 respectively for maximum and minimum values.

We will obtain:

$b - a = 12$ and $a + b = 34$

Solving: $a=11$ and $b=23$

Multiplying both together will give the final answer of $253$ .

Answer. $a=11$, $b=23$. $a\times b=253.$

It is well-known that $\cos^{2}x=1-\sin^{2}x.$ So the equation can equivalent to $1-\sin^{2}x-a\sin x+b.$ It can be seen that $-\sin^{2}x-a\sin x+b$ ranges between $11$ and $33,$ which differs by $22$.

Now, since $b$ is constant, we know that $-\sin^{2}x-a\sin x=-\sin x(\sin x+a\sin x)$ also have range (i.e. difference between minimum value and maximum value) of 22. Let $\sin x=z,$ we know that $z$ is everything in the interval $[-1, 1].$ Consider the number $z(z+a)$. Therefore, $z(z+a)$ has a range of 22 when we consider all $z$ in the interval of $[-1, 1].$ Since $a>5,$ we know that $z(z+a)$ has minimum value when $z=\frac {-a}{2}<\frac {-5}{2},$ which is impossible since $z\ge -1.$ This further implies that since $\frac {d}{dz}z(z+a)=2z+a,$ which is obviously greater than 0 since $2z+a\ge -2+a>-2+5=3.$ So $z(z+a)$ is strictly increasing for $z\in [-1, 1].$

Therefore $z(z+a)$ has minimum value when $z=-1,$ and thus $z(z+a)=-1(a-1)=1-a$ and has maximum value when $z=1,$ thus $z(z+a)=1(a+1)=a+1.$ Since $22=(a+1)=(1-a)=2a,$ so $a=11.$

Now when $\sin x$ is minimum when $x=270^{\circ}$ so $\sin x=-1.$ $\sin x$ is maximum when $x=90^{\circ}$ so $\sin x=1.$ In both cases $\cos x=\cos^{2} x=0,$ so $12=\cos^{2} 90-11\sin 90+b=-11+b, 34=\cos^{2} 270-11\sin 270+b=11+b.$ Therefore $b=23.$ This completes the proof.

y=\frac{a^2}{4}+b+1-(\sin{x}+\frac{a}{2})^2 Maximum of y is when \sin{x}=-1 as a is integer greater than 5 \Rightarrow a+b=34 Minimum of y is when \sin{x}=+1 \Rightarrow b-a=12 From a+b=34 and b-a=12 \Rightarrow a=11 and b=23 and ab=253

Given, $f(x)=cos^{2}x-a \times sinx+b$

which can be further written as: $f(x)=1-sin^{2}x-a \times sinx+b$

Let $sinx=y$

Then, $f(y)=1-y^{2}-a \times y+b$

The two extreme values of $f(y)$ may be obtained by substituting $y=1$ and $y=-1$ as maximum and minimum values of $y=sinx$ are $+1$ and $-1$

Therefore

$f(1)=1-1-a+b= b-a$

and

$f(-1)=1-1+a+b= a+b$

Since $a$ and $b$ are positive integers,

therefore

$f_{max}=a+b=34$ ----------------------------------------------- $1$

and

$f_{min}=b-a=12$ -------------------------------------------------- $2$

Solving eq. $1$ and $2$ ,

$a=11$ and $b=23$

Therefore $a \times b=23 \times 11=253$

$y = \cos^2{x} - a\sin{x} + b$
$= -\sin^2{x} - a\sin{x} + (b+1)$
$= -y^2 - ay + (b+1), y\in [-1,1]$ by the Pythagorean identities.
The vertex of this parabola has an x-value of
$-\frac{a}{2} < -\frac{5}{2} < -1$ as given in the problem.
Also, the parabola opens downward so is monotone decreasing on $[-1,1]$ .
This gives
$a+b = 34, -a+b = 12$ $a = 11, b = 23, ab = \boxed{253}$

easy yet again write cos^2 x as 1-sin^2 x then this expression as max value when sinx=1 and minimum value when sinx=0; solve get answer the answer is 253

Using cos^2x = 1 - sin^2x, $f(x) = (1 - sin^2x) - asinx + b = -sin^2x - asinx + b + 1$ The extrema of f(x) are the extrema of the function $g(x) = sin^2x + asinx = sinx(sinx + a)$ since f(x) = -g(x) + a constant. Since a is positive, the maximum of g(x) is where sin(x) = 1, so that $g(x) = 1 + a$ And since a > 1, the minimum of g(x) is where sin(x) = -1, so that $g(x) = 1 - a$ Plugging into f(x): $f(x_max) = -(1 - a) + b + 1 = b + a = 34$ $f(x_min) = -(1 + a) + b + 1 = b - a = 12$ $b = 23, a = 11$ $a*b = 253$

The relevant parameter for the behavior of maxima and minima of $f(x)$ is $a$ ( $b$ just displaces the function up and down).

For $a>1$ , the extremes of $f(x)$ are the same as those of $g(x)=b-a\sin{x}$ ( $b+a$ and $b-a$ ), since $\cos^2{x}=0$ when $\sin{x}=\pm1$ . These two functions are almost identical for $a\gg 1$ . For small values of $a$ , the maxima become wider and flatter and the behavior changes dramatically when $a=1$ , when the effect of the doble frequency of $\cos^2{x}$ becomes apparent.

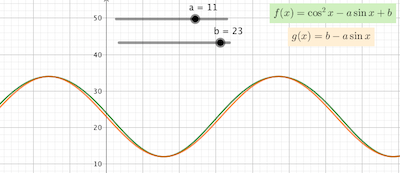
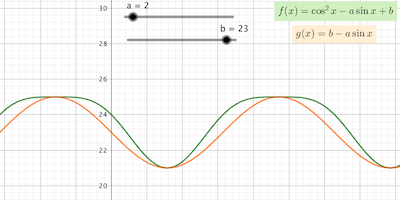
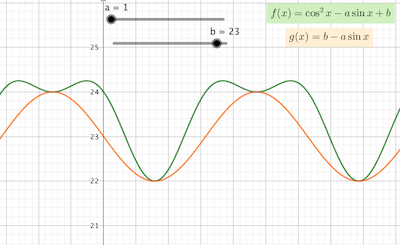
For the values given, $b+a=34; b-a=12\implies a=11, b=23$ and $a\times b=\boxed{253}$ .

take the derivative of the original function, which is cosx(-2sinx-a). In order for this derivative to be 0, cosx must be 0, and thereby x = pi/2 + k * pi. Put the values in the second derivative, we find that when x = pi/2 + 2kpi, the second derivative is > 0, which implies that this is the minimum, and that when x = pi/2 + (2k+1) pi, the second derivative is < 0, meaning that this is the maximum. Put the values of x into the original function, we have {b - a = 12, a + b = 34}. Therefore, a = 11 and b = 23, and mutiplying both get answer of 253

max value: add as much, subtract the least. we can obtain that by setting x=3pi/2 which gets us a+b=34.

min value: add the least, subtract as much. we can obtain that by setting x=pi/2 which gets us -a+b=12.

you can the solve for a and b using systems of linear equations.

as to how i got the values for x, you just need to be comfortable with your understanding of trigonometry.

$Since ~a>Cos^2X, ~~~ \text {and b remains add,} \\ \text {it is only aSinX that decides Max. and Min.} \\ \text{Clearly SinX has to be } \pm 1 ~~for~ maximum ~effect, ~~~~~ X= \pm \dfrac \pi 2 .\\ f(-\dfrac \pi 2 )=0+a+b=34,~~and~~ f(+\dfrac \pi 2 )=0-a+b=12.\\\implies ~a=11,~~b=23. ~~~a\times b =~~ \large \color{#D61F06}{253}\\~~\\\text {The above and similar non-calculus approaches are the best.} \\\text {I give below another angle of approaching the solution.}\\\text {Since a and b and Max. and Min. are all integers, and a>5,} \\ \text {any irrational SinX can not be compensated by } Cos^2X . \\\implies ~SinX \text { be rational. So X can take values } 0, ~\pm \dfrac \pi 6 , \pm \dfrac \pi 2.\\ \text {Extreme values can be obtained only with } \pm \dfrac \pi 2. \\\text{Thus the solution.}\\\text{Note two points.} \pm \dfrac \pi 6 ~\text{ is possible because we have } Cos^{\color{#3D99F6}{2}} X.\\ \because Cos^{\color{#3D99F6}{2}} X, \text { Qud. II and III will give the same results as I and IV.}$

Derivate the function: f'(x)=- $2cosxsinx-acosx$ The two solutions for are x= $\frac{\pi}{2}$ and x= $-\frac{\pi}{2}$ . Another one is sinx= $-\frac{a}{2}$ but it's impossibile since a and b are >5. For the Fermat's theorem, there are a minimum and a maximum in those points, which are $f(\frac{\pi}{2})=11$ and $f(\frac{\pi}{2})=23$ . $ab=253$

Highest negative value of sin x is equal to -1 when x=270 degree. Then y= cos^270-a sin (270) + b = 34. 0+a (1) + b=34. (cos^270=0 and sin270=-1) a+b=34..........(1) . Highest positive value of sin x =1 when x=90 degree. Then y=cos^90 - a sin (90)+ b=12. (cos^90=0 and sin 90=1). -a+b=12 .............(2) Solving equation (1) and (2), a=11 and b=23 Therefore a b=11 23=253.

First notice that $cos^2(x)$ will have a max at 1 on multiples of $pi$ and a min of 0 on multiples of $pi/2$ . Next notice that sin will have a max of 1 and a min of -1 and they will always fall when x is a multiple of $pi/2$ . What this tells us is, if a is very large at all, the max and mins of the whole function will fall on the multiples of $pi/2$ and we can treat it as though it were just a sin function as that part will eclipse the $cos^2(x)$ . Next we can solve for the value of a by looking at the difference of the max and the min and thinking of our whole function as a scaled and shifted sin function. Since the $max - min = 34 - 12 = 22$ we know that $2a = 22$ so $a = 11$ . Finally we can use the offset of b to move the function to the right spot. Without the offset the min would be -11 and the max would be +11 so we know that $b = 23$ . Finally multiply $a*b = 11*23 = 253$

We take the derivative of y:

$y' = \sin x*2 \cos x - a*\cos x + 0$

If y = f(x) reaches a maximum or minimum, f'(x) = 0:

$0 = 2*\sin x*\cos x - a*\cos x = \cos x*(2\sin x - a)$

Notice that since a > 5, (2sin(x) - a) < 0, so cos(x) = 0. Thus, y reaches a critical point at $x = \pi /2$ or $3\pi /2$ (or any equivalent angles).

When $-\pi /2 < x < \pi /2$ , f'(x) < 0, so y reaches a minimum at $x = \pi /2$ . Thus, $12 = (0)^2 - a*(1) + b = -a + b$

When $\pi /2 < x < 3\pi /2$ , f'(x) > 0, so y reaches a maximum at $x = 3\pi /2$ , so $34 = (0)^2 - a*(-1) + b = a + b$

Thus, we have a + b = 34 and -a + b = 12. Adding these, we get 2b = 46, so b = 23, and a = 11, so a * b = 253.

We note that | cos(x) | <= 1 and | sin(x)| =1. Also we know that if sin(x) =1 or -1 then cos(x)=0. Since a, b > 5 for a maximum value 34 we get: either 34=1+b or 34=0+a + b (if sin(x)=-1). Obviously the second case occurs, since a>1. With the same arguments for a minimum 12 we get either 12=1+b or 12=0-a + b. Since 1 > -a we keep the second equation. So we have only to solve the system { a+b=34 and b-a=12}. Since we get a=11 and b=23, the product a x b is 253.

The max of sin(x) is 1, and the min of sin(x) is -1. The max of cos^2(x) is 1 and the min of cos^2(x) = 0.

First we find the minimum by zeroing out certain values. We want to make this function as low as possible, and because sin(x) is 0 whenever cos(x) is 1, and vice versa, we have to choose whether we want the cos^2(x) term or the a sin(x) term for the max. since a sin(x) is significantly greater than cos^2(x), we choose values that maximize and minimize a*sin(x) while leaving cos^2(x) zero.

If sin(x) =1, then cos^2(x) = 0, so y1 = b-a.

if sin(x) = -1 then cos^2(x) = 0 and y2 = a+b

Since y1<b and y2>b it follows that y2>y1.

Since these are our maximums and minimums, we have found that y2 is the maximum and y1 is the minimum.

Therefore y2 = 34 and y1 = 12.

y2 = b+a = 34 y1 = b - a = 12

Adding the equations 2b = 56 b = 23.

If b = 23 and b-a = 12, a must be 11.

Therefore a b = 23 11 = 253.

since b is a constant; the maximum and minimum value of the function depends on the part (cos^2x-asinx). Let us call this part as G.

when x=0 ;G=1 when x=90 ;G=-a when x=180; G=1 when x=270; G=a

so the maximum value of G is a and the minimum value is -a. substituting the value we get two equations b+a=34 and b-a=12. solving these two ,we get a=11 & b=23. so a.b=253.

sine and cosine have ranges of +/-1, so the extreme values for y will be reached when cos(x)=+/-1 or sin(x)=+/-1 when sin(x)=+/-1, cos(x)=0, so y = +/-a+b when cos(x)= +/-1, sin(x)=0, so y = b

a and b are both positive integers, so -a+b < b and a+b>b therefore the extreme values for y will be -a+b and a+b

If we solve {a+b=34; -a+b=12} we get a=11, b=23 which are the values of the parameters which will give the appropriate min and max values for y.

The product ab = 253

\cos^2\x - asinx can have varying values, while b must be constant. Assuming that x = \90^\circ causes \cos^2\x to be equal to 0, while -asinx is the only remaining variable that determines the function's range. At x = \90^\circ, sinx = 1, so y = b - a (minimum value of 12). Similarly, at x = \270^\circ, y = b + a (maximum value of 34). Solving for a & b simultaneously gives b = 23, a = 11, and their product is 253.

The maximum or minimum occurs when the first derivative is 0. y' = -2 cos x sin x - a cos x Factoring gives y' = cos x(2 sin x - a) Since our equation is periodic over period 2pi, we see cos x = 0 for x = pi/2, 3pi/2. 2 sin x = a only when |a| <= 2 which clearly would not allow the maximum and minimum to differ so much because cos^2 (x) only varies by +-1 so the variance is coming from the (a sin x) term hence we know a > 2 and we can ignore these 0's.

That means our minimum is at x = pi/2 and maximum is at x = 3pi/2. From here, we have 2 linear equations with a and b that can easily be solved to give a = 11, b = 23. a*b = 253

As we know from given eqn y=cos^2x-asinx+b
for maximum value sinx should be smallest i.e. -1 so 1st equation will become a+b=34 ------- (1)

for minimum value sinx should be maximum i.e. +1 so 2nd equation will become

b-a=12 --------(2)

solving eqn (1) and (2) we get

b=23

a=11

so a X b=253

f(x) is maximum when sinx=-1 and cosx=0 => b+a=34

f(x) is minimum when sinx=1 and cosx=0 => b-a=12

solving the two linear equations, we get a=11 and b=23.

hence axb=23x11=253

a + b = 34 -a + b = 12

Solving the systems of equations by elimination a = 11 and b = 23

A. Quinones Cidra, Puerto Rico