Maximum Angle of Sight
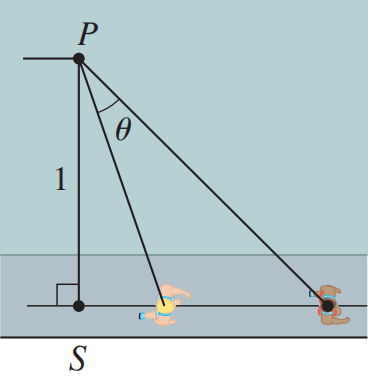
An observer stands at a point P , one unit away from a track. Two runners start at the point S in the figure and run along the track. One runner runs three times as fast as the other.
Find the maximum value of the observer’s angle of sight θ between the runners.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
tan y = x , tan ( θ + y ) = 3 x
tan θ + y = 1 − tan y tan θ tan θ + tan y = 3 x
tan θ = 3 x 2 + 1 2 x = 3 x + 1 / x 2 ≥ 3 1 by AM-GM, when θ = 6 π
Let the position of the slower runner be Q and that of the faster runner be R , and let ∣ S Q ∣ = x > 0 . Then ∣ S R ∣ = 3 x and
θ = ∠ R P S − ∠ Q P S = arctan ( ∣ S R ∣ / ∣ S P ∣ ) − arctan ( ∣ S Q ∣ / ∣ S P ∣ ) = arctan ( 3 x ) − arctan ( x ) .
Differentiating θ with respect to x we see that
d x d θ = 1 + 9 x 2 3 − 1 + x 2 1 = ( 1 + 9 x 2 ) ( 1 + x 2 ) 3 ( 1 + x 2 ) − ( 1 + 9 x 2 ) = ( 1 + 9 x 2 ) ( 1 + x 2 ) 2 − 6 x 2 ,
which equals 0 when 2 − 6 x 2 = 0 ⟹ x 2 = 3 1 ⟹ x = 3 1 .
Now since θ ≥ 0 ∀ x ≥ 0 , θ ( 0 ) = 0 and x → ∞ lim θ ( x ) = 0 , we know that the critical point found above will represent a maximum, and so the desired maximum is
θ max = arctan ( 3 ) − arctan ( 1 / 3 ) = 6 0 ∘ − 3 0 ∘ = 3 0 ∘ .